Question

【题目】【阅读理解】对于任意正实数a、b，

∵（－）2≥0，∴a－2＋b≥0，

∴a＋b≥2，（只有当a=b时，a＋b等于2）．

【获得结论】在a＋b≥2（a、b均为正实数）中，若ab为定值p，

则a＋b≥2，只有当a=b时，a＋b有最小值2．

根据上述内容，回答下列问题：（1）若>0，只有当= 时，m+有最小值 ．

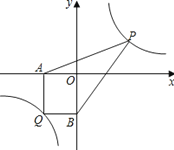
【探索应用】（2）已知点Q(－3，－4)是双曲线y=上一点，过Q作QA⊥x轴于点A，作QB⊥y轴于点B．点P为双曲线y=（x＞0）上任意一点，连接PA，PB，求四边形AQBP的面积的最小值．

Answer 1

【答案】(1)、m=2，最小值为4；(2)、24.

【解析】试题分析：(1)、根据题意可得：m=，从而求出m的值，然后将m的值代入代数式得出最小值；(2)、设点P的坐标为（x，），然后求出四边形的面积得出答案.

试题解析：(1)、根据题意可得：m=解得：m=2 则最小值为：m+=2+2=4

(2)、连接PQ，设P（x，），∴S四边形AQBP==≥12+12=24

∴最小值为24