题目内容
【题目】如图，正方形ABCD的边长为3，延长CB到点M，使BM=1，连接AM，过点B作BN⊥AM，垂足为N，O是对角线AC，BD的交点，连接ON，则ON的长为 ．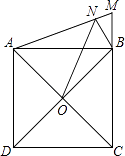 
【答案】
【解析】解：∵AB=3，BM=1，
∴AM= 
，
∵∠ABM=90°，BN⊥AM，
∴△ABN∽△BNM∽△AMB，
∴AB2=AN×AM，BM2=MN×AM，
∴AN= 
，MN= 
，
∵AB=3，CD=3，
∴AC= 
，
∴AO= 
，
∵ 
， 
，
∴ 
，且∠CAM=∠NAO
∴△AON∽△AMC，
∴ 
，
∴ON= ．
故答案为： ．
由条件可证得△ABN∽△BNM∽△ABM，且可求得AM= ，利用对应线段的比相等可求得AN和MN，进一步可得到 ，且∠CAM=∠NAO，可证得△AON∽△AMC，利用相似三角形的性质可求得ON．
练习册系列答案
相关题目
