题目内容
观察规律:用同样大小的黑色棋子按图中所示的方式摆图形,观察图中棋子的摆放规律,猜想第n个图形需棋子 枚(用含n的代数式表示,n为正整数).


考点:规律型:图形的变化类
专题:
分析:观察图形得到第1个图形所需棋子数=3×2-3=3×1;第2个图形所需棋子数=3×3-3=6=3×2;第3个图形所需棋子数=3×4-3=9=3×3;于是得到图形中棋子的个数等于该图的序号数的3倍,则第4个图形所需棋子数=3×4;由此可得第n个图形所需棋子数=3n.
解答:解:第1个图形所需棋子数=3×2-3=3×1;
第2个图形所需棋子数=3×3-3=6=3×2;
第3个图形所需棋子数=3×4-3=9=3×3;
第4个图形所需棋子数=3×5-3=12=3×4;
第5个图形所需棋子数=3×5=15;
…
第n个图形所需棋子数=3n.
故答案为:3n.
第2个图形所需棋子数=3×3-3=6=3×2;
第3个图形所需棋子数=3×4-3=9=3×3;
第4个图形所需棋子数=3×5-3=12=3×4;
第5个图形所需棋子数=3×5=15;
…
第n个图形所需棋子数=3n.
故答案为:3n.
点评:本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
下列根式中属于最简二次根式的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法正确的是( )
| A、两名同学5次平均分相同,则方差较大的同学成绩更稳定 |
| B、一组数据3,4,4,6,8,5的众数是4 |
| C、必然事件的概率是100%,随机事件的概率是50% |
| D、为防止H7N9流感,对确认患者的密切接触者采用抽样调查的方法 |
 某大型生活超市销售一种进口奶粉A,从去年1至7月,这种奶粉的进价一路攀升,每罐A奶粉的进价y1与月份x(1≤x≤7,且x为整数),之间的函数关系式如下表:
某大型生活超市销售一种进口奶粉A,从去年1至7月,这种奶粉的进价一路攀升,每罐A奶粉的进价y1与月份x(1≤x≤7,且x为整数),之间的函数关系式如下表: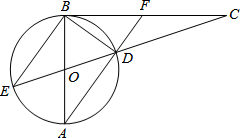 如图,AB是⊙O的直径,BC切⊙O于点B,连接CO并延长,交⊙O于点D、E,连接AD并延长,交BC于点F.
如图,AB是⊙O的直径,BC切⊙O于点B,连接CO并延长,交⊙O于点D、E,连接AD并延长,交BC于点F. 如图,在平面直角坐标系中,A(-3,-1),B(-3,-3),C(-2,-3),先把△ABC向右平移4个单位,得到△A1B1C1.
如图,在平面直角坐标系中,A(-3,-1),B(-3,-3),C(-2,-3),先把△ABC向右平移4个单位,得到△A1B1C1.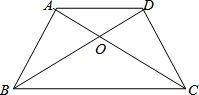 如图,四边形ABCD的对角线AC、BD相交于点O,OA=OD,OB=OC,则图中全等的三角形共有
如图,四边形ABCD的对角线AC、BD相交于点O,OA=OD,OB=OC,则图中全等的三角形共有 如图,△ABC中,AB=AC,∠BA0=45°,△ABC内接于⊙0,D为⊙O上一点,过点D作⊙O的切线交BC的延长线于E,若DE⊥BC,AD=2
如图,△ABC中,AB=AC,∠BA0=45°,△ABC内接于⊙0,D为⊙O上一点,过点D作⊙O的切线交BC的延长线于E,若DE⊥BC,AD=2