题目内容
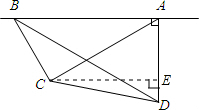
 (2013•石景山区一模)如图,一架飞机由A向B沿水平直线方向飞行,在航线AB的正下方有两个山头C、D.飞机在A处时,测得山头D恰好在飞机的正下方,山头C在飞机前方,俯角为30°.飞机飞行了6千米到B处时,往后测得山头C、D的俯角分别为60°和30°.已知山头D的海拔高度为1千米,求山头C的海拔高度.(精确到0.01千米,已知
(2013•石景山区一模)如图,一架飞机由A向B沿水平直线方向飞行,在航线AB的正下方有两个山头C、D.飞机在A处时,测得山头D恰好在飞机的正下方,山头C在飞机前方,俯角为30°.飞机飞行了6千米到B处时,往后测得山头C、D的俯角分别为60°和30°.已知山头D的海拔高度为1千米,求山头C的海拔高度.(精确到0.01千米,已知| 3 |
分析:首先在Rt△ABD中求出AD的长度,然后根据∠ABC=60°,∠BAC=30°,求出∠ACB=90°,在Rt△ABC中求出AC的长度,根据A处山头C的俯角为30°,求出AE的长度,继而可求出山头C的海拔高度.
解答:解:在Rt△ABD中,∵∠ABD=30°,
∴AD=AB•tan30°=6×
=2
,
∵∠ABC=60°,∠BAC=30°,
∴∠ACB=90°,
∴AC=AB•cos30°=6×
=3
,
过点C作CE⊥AD于点E,
则∠CAE=60°,AE=AC•cos60°=
,
∴DE=AD-AE=2
-
=
,
∴山头C的海拔高度为1+
≈1+
=1.87(千米).
答:山头C的海拔高度1.87千米.
∴AD=AB•tan30°=6×
| ||
| 3 |
| 3 |

∵∠ABC=60°,∠BAC=30°,
∴∠ACB=90°,
∴AC=AB•cos30°=6×
| ||
| 2 |
| 3 |
过点C作CE⊥AD于点E,
则∠CAE=60°,AE=AC•cos60°=
3
| ||
| 2 |
∴DE=AD-AE=2
| 3 |
3
| ||
| 2 |
| ||
| 2 |
∴山头C的海拔高度为1+
| ||
| 2 |
| 1.732 |
| 2 |
答:山头C的海拔高度1.87千米.
点评:本题考查了解直角三角形的应用,难度一般,解答本题的关键是在直角三角形中分别利用解直角三角形的方法求出AD,AC的值.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
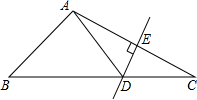 (2013•石景山区二模)如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为( )
(2013•石景山区二模)如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为( ) (2013•石景山区二模)如图,AB是⊙O的直径,C是⊙O上的一点,若AC=8,AB=10,OD⊥BC于点D,则BD的长为( )
(2013•石景山区二模)如图,AB是⊙O的直径,C是⊙O上的一点,若AC=8,AB=10,OD⊥BC于点D,则BD的长为( )