题目内容
如图,已知等边△ABC,D是边BC的中点,过D作DE∥AB于E,连接BE交AD于D1;过D1作D1E1∥AB于E1,连接BE1交AD于D2;过D2作D2E2∥AB于E2,…,如此继续,若记S△BDE为S1,记 为S2,记
为S2,记 为S3…,若S△ABC面积为Scm2,则Sn= cm2(用含n与S的代数式表示)
为S3…,若S△ABC面积为Scm2,则Sn= cm2(用含n与S的代数式表示)
【答案】分析:根据D是边BC的中点,过D作DE∥AB,得到E为AC的中点,BE⊥AC,设△ABC的高是h,根据三角形的面积公式求出s1= •
• BC•
BC• AD=
AD= s=
s= ,根据DE∥AB,D1E1∥AB,得到
,根据DE∥AB,D1E1∥AB,得到 =
= =2=
=2= ,求出s2=
,求出s2= ,同理s3=
,同理s3= s=
s= ,进而得出sn=
,进而得出sn= ,即得到答案.
,即得到答案.
解答:解:∵D是边BC的中点,过D作DE∥AB,
∴E为AC的中点,BE⊥AC,
设△ABC的高是h,

过E作EM⊥BC于M,
∵BD=DC,DE∥AB,
∴AE=EC,
∵AD⊥BC,EM⊥BC,
∴AD∥EM,
∴DM=MC,
∴EM= AD=
AD= h,
h,
∴s1= •
• BC•
BC• AD=
AD= s=
s= ,
,
∵DE∥AB,D1E1∥AB,
∴ =
= =2=
=2= ,
,
∴s2= •
• AE•h-
AE•h- •
• AE•
AE• h=
h= s=
s= ,
,
同理s3= s=
s= ,
,
…
sn= ,
,
故答案为: .
.
点评:本题主要考查对三角形的面积,平行线分线段成比例定理,相似三角形的性质,等边三角形的性质,三角形的中位线定理等知识点的理解和掌握,能根据求出的结果找出规律是解此题的关键.
 •
• BC•
BC• AD=
AD= s=
s= ,根据DE∥AB,D1E1∥AB,得到
,根据DE∥AB,D1E1∥AB,得到 =
= =2=
=2= ,求出s2=
,求出s2= ,同理s3=
,同理s3= s=
s= ,进而得出sn=
,进而得出sn= ,即得到答案.
,即得到答案.解答:解:∵D是边BC的中点,过D作DE∥AB,
∴E为AC的中点,BE⊥AC,
设△ABC的高是h,

过E作EM⊥BC于M,
∵BD=DC,DE∥AB,
∴AE=EC,
∵AD⊥BC,EM⊥BC,
∴AD∥EM,
∴DM=MC,
∴EM=
 AD=
AD= h,
h,∴s1=
 •
• BC•
BC• AD=
AD= s=
s= ,
,∵DE∥AB,D1E1∥AB,
∴
 =
= =2=
=2= ,
,∴s2=
 •
• AE•h-
AE•h- •
• AE•
AE• h=
h= s=
s= ,
,同理s3=
 s=
s= ,
,…
sn=
 ,
,故答案为:
 .
.点评:本题主要考查对三角形的面积,平行线分线段成比例定理,相似三角形的性质,等边三角形的性质,三角形的中位线定理等知识点的理解和掌握,能根据求出的结果找出规律是解此题的关键.

练习册系列答案
相关题目
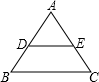
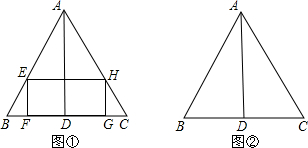
 (2013•黄浦区二模)如图,已知等边△ABC的边长为1,设
(2013•黄浦区二模)如图,已知等边△ABC的边长为1,设
 如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动
如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动