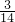Question

相邻两边不等的长方形ABCD，中心为O．在点A，B，C，D，O五个点构成的三角形中，任取两个三角形，面积相等的概率为（　　）

• A．

  3

  7

• B．

  3

  14

• C．

  1

  2

• D．

  4

  7

Answer 1

分析：首先根据题意可求得相邻两边不等的长方形ABCD中共有8个三角形，且S_△AOB=S_△AOD=S_△COD=S_△BOC，S_△ABC=S_△BCD=S_△ACD=S_△BAD，又由任取两个三角形，共有8×7=56种等可能的结果，面积相等的有24种情况，利用概率公式即可求得答案．

解答：解：如图：共有8个三角形，
则任取两个三角形，共有8×7=56种等可能的结果；
∵四边形ABCD是矩形，
∴OA=OC，OB=OD，AC=BD，
∴OA=OB=OC=OD，
∴S_△AOB=S_△AOD=S_△COD=S_△BOC，S_△ABC=S_△BCD=S_△ACD=S_△BAD，
∴任取两个三角形，面积相等的有：3×8=24（种），
∴任取两个三角形，面积相等的概率为：

24

56

=

3

7

．
故选A．

点评：此题考查了矩形的性质与乘法公式求概率的知识．此题难度适中，解题的关键是掌握乘法公式的应用．