题目内容
 已知如图,AB∥DC,∠D=90°,BC=
已知如图,AB∥DC,∠D=90°,BC= ,AB=4,
,AB=4,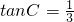 ,求梯形ABCD的面积.
,求梯形ABCD的面积.
 解:作BE⊥CD于点E,则DE=AB=4,
解:作BE⊥CD于点E,则DE=AB=4,∵tanC=

∴cosC=
 ,sinC=
,sinC=
在直角△BCE中,cosC=
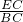 ,即
,即 =
= ;
;sinC=
 =
= ,即
,即 =
=
∴EC=3,BE=1
∴DC=DE+EC=4+3=7,
梯形ABCD的面积是:
 ×(AB+CD)•BE=
×(AB+CD)•BE= ×(4+7)×1=
×(4+7)×1= .
.分析:作BE⊥CD于点E,在直角△BCE中根据三角函数即可求得BE与EC的长,进而就可以求出梯形的面积.
点评:直角梯形的问题可以转化为直角三角形与矩形的问题解决,转化的方法是作高线.

练习册系列答案
相关题目
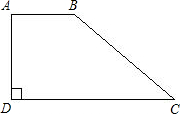 已知如图,AB∥DC,∠D=90°,BC=
已知如图,AB∥DC,∠D=90°,BC=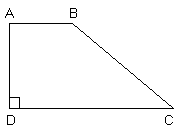

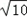 ,AB=4,
,AB=4,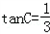 ,求梯形ABCD的面积.
,求梯形ABCD的面积.