题目内容
对于结论:当a+b=0时,a3+b3=0也成立.若将a看成a3的立方根,b看成是b3的立方根,由此得出这样的结论:“如果两数的立方根互为相反数,那么这两数也互为相反数”.(1)试举一个例子来判断上述结论的猜测是否成立?
(2)若
| 3 | 3-2x |
| 3 | x+5 |
| 2x |
分析:(1)这个结论很简单,可选择
+
=0,则2与-2互为相反数进行说明.
(2)利用(1)的结论,列出方程(3-2x)+(x+5)=0,从而解出x的值,代入可得出答案.
| 3 | 2 |
| 3 | -2 |
(2)利用(1)的结论,列出方程(3-2x)+(x+5)=0,从而解出x的值,代入可得出答案.
解答:解:(1)答案不唯一.如
+
=0,则2与-2互为相反数;
(2)由已知,得(3-2x)+(x+5)=0,
解得x=8,
∴1-
=1-
=1-4=-3.
| 3 | 2 |
| 3 | -2 |
(2)由已知,得(3-2x)+(x+5)=0,
解得x=8,
∴1-
| 2x |
| 16 |
点评:本题考查立方根的知识,难度一般,注意一个数的立方根有一个,它和这个数正负一致,本题的结论同学们可以记住,以后可直接运用.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
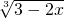 与
与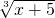 的值互为相反数,求
的值互为相反数,求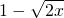 的值.
的值.