Question

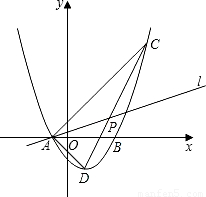
（2009•乐山）如图，一次函数y=-x-2的图象分别交x轴、y轴于A、B两点，P为AB的中点，PC⊥x轴于点C，延长PC交反比例函数y=（x＜0）的图象于点Q，且tan∠AOQ=．
（1）求k的值；
（2）连接OP、AQ，求证：四边形APOQ是菱形．

Answer 1

【答案】分析：（1）由一次函数解析式确定A点坐标，进而确定C，Q的坐标，将Q的坐标代入反比例函数关系式可求出k的值．
（2）由（1）可分别确定QC=CP，AC=OC，且QP垂直平分AO，故可证明四边形APOQ是菱形．
解答：（1）解：∵y=-x-2
令y=0，得x=-4，即A （-4，0）
由P为AB的中点，PC⊥x轴可知C点坐标为（-2，0）
又∵tan∠AOQ=可知QC=1
∴Q点坐标为（-2，1）
将Q点坐标代入反比例函数得：1=，
∴可得k=-2；

（2）证明：由（1）可知QC=PC=1，AC=CO=2，且A0⊥PQ
∴四边形APOQ是菱形．
点评：本题考查了待定系数法求函数解析式，又结合了几何图形进行考查，属于综合性比较强的题目，有一定难度．