Question

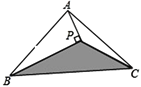
【题目】如图，扇形AOB中，半径OA=2，∠AOB=120°，C是 的中点，连接AC、BC，则图中阴影部分面积是（ ）
A. ﹣2
B. ﹣2
C. ﹣
D. ﹣

Answer 1

【答案】A
【解析】解：连接OC，过O作OM⊥AC于M，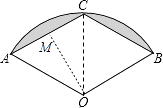
∵∠AOB=120°，C为弧AB中点，
∴∠AOC=∠BOC=60°，
∵OA=OC=OB=2，
∴△AOC、△BOC是等边三角形，
∴AC=BC=OA=2，AM=1，
∴△AOC的边AC上的高是 = ，
△BOC边BC上的高为 ，
∴阴影部分的面积是 ﹣ ×2× + ﹣ ×2× = π﹣2 ，
故选：A．
【考点精析】利用扇形面积计算公式对题目进行判断即可得到答案，需要熟知在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）．