Question

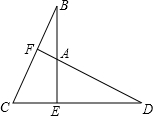已知：BE⊥CD，BE=DE，BC=DA，AD与BC有何位置关系？

Answer 1

分析：根据SAS证△BEC≌△DEA，推出∠B=∠D，根据∠D+∠DAE=90°推出∠B+∠BAF=90°，求出∠BFA=90°，根据垂直定义求出即可．

解答：解：AD⊥BC，
理由是：∵BE⊥CD，
∴∠BEC=∠DEA=90°，
∵在△BEC和△DEA中

BE=DE ∠BEC=∠DEA CE=AE

，
∴△BEC≌△DEA（SAS），
∴∠B=∠D，
∵∠BEC=∠DEA=90°，
∴∠D+∠DAE=90°，
∵∠BAF=∠DAE，
∴∠B+∠BAF=90°，
∴∠BFA=180°-90°=90°，
∴AD⊥BC．

点评：本题考查了全等三角形的性质和判定，三角形的内角和定理，垂直定义等知识点，注意：全等三角形的对应角相等，全等三角形的判定定理有SAS，ASA，AAS，SSS．