Question

如图，在平面直角坐标系xOy中，正比例函数y=x的图象与一次函数y=kx－k的图象的交点坐标为A（m，2）．

（1）求m的值和一次函数的解析式；

（2）设一次函数y=kx－k的图象与y轴交于点B，求△AOB的面积；

（3）直接写出使函数y=kx－k的值大于函数y=x的值的自变量x的取值范围．

                 

Answer 1

解：（1）∵点A（m，2）正比例函数y=x的图象上，

∴m=2．

∴点A的坐标为（2，2）．

∵点A在一次函数y=kx－k的图象上，

∴2=2k－k，∴k=2．

∴一次函数y=kx－k的解析式为y=2x－2．

（2）过点A作AC⊥y轴于C.

∵A（2，2）， ∴AC=2.  

∵当x=0时，y=－2，

∴B（0，－2），

∴OB=2.  

∴S_△AOB=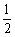×2×2=2. ……………………………………………………5分

（3）自变量x的取值范围是x＞2．…………………………………………6分