题目内容
 如图,⊙O的半径OP=10cm,弦AB过OP的中点Q,且∠OQB=45°,则弦AB的长为________.
如图,⊙O的半径OP=10cm,弦AB过OP的中点Q,且∠OQB=45°,则弦AB的长为________.
5 cm
cm
分析:过O作OC⊥AB,连接OA,由垂径定理得到C为AB的中点,即AB=2AC,由Q为OP中点,求出OQ的长,在等腰直角三角形OCQ中,利用锐角三角函数定义求出OC的长,在直角三角形AOC中,利用勾股定理求出AC的长,即可求出AB的长.
解答: 解:过O作OC⊥AB,连接OA,由垂径定理得到C为AB的中点,即AB=2AC,
解:过O作OC⊥AB,连接OA,由垂径定理得到C为AB的中点,即AB=2AC,
∵⊙O的半径OP=10cm,弦AB过OP的中点Q,
∴OQ=5cm,
∵∠OCQ=90°,∠OQB=45°,
∴△OCQ为等腰直角三角形,
∴OC=OQsin45°= cm,
cm,
在Rt△AOC中,根据勾股定理得:AC= =
= cm,
cm,
则AB=2AC=5 cm.
cm.
故答案为:5 cm.
cm.
点评:此题考查了垂径定理,勾股定理,等腰直角三角形的性质,以及锐角三角函数定义,熟练掌握垂径定理是解本题的关键.
 cm
cm分析:过O作OC⊥AB,连接OA,由垂径定理得到C为AB的中点,即AB=2AC,由Q为OP中点,求出OQ的长,在等腰直角三角形OCQ中,利用锐角三角函数定义求出OC的长,在直角三角形AOC中,利用勾股定理求出AC的长,即可求出AB的长.
解答:
 解:过O作OC⊥AB,连接OA,由垂径定理得到C为AB的中点,即AB=2AC,
解:过O作OC⊥AB,连接OA,由垂径定理得到C为AB的中点,即AB=2AC,∵⊙O的半径OP=10cm,弦AB过OP的中点Q,
∴OQ=5cm,
∵∠OCQ=90°,∠OQB=45°,
∴△OCQ为等腰直角三角形,
∴OC=OQsin45°=
 cm,
cm,在Rt△AOC中,根据勾股定理得:AC=
 =
= cm,
cm,则AB=2AC=5
 cm.
cm.故答案为:5
 cm.
cm.点评:此题考查了垂径定理,勾股定理,等腰直角三角形的性质,以及锐角三角函数定义,熟练掌握垂径定理是解本题的关键.

练习册系列答案
相关题目
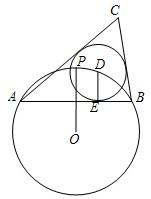 如图,⊙O的半径为1,点P是⊙O上一点,弦AB垂直平分线段OP,点D是
如图,⊙O的半径为1,点P是⊙O上一点,弦AB垂直平分线段OP,点D是
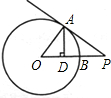 如图,⊙O的半径OA=3,P是⊙O外一点,OP交⊙O于点B,PB=2,PA=4,
如图,⊙O的半径OA=3,P是⊙O外一点,OP交⊙O于点B,PB=2,PA=4,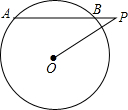 (2013•本溪)如图,⊙O的半径是3,点P是弦AB延长线上的一点,连接OP,若OP=4,∠APO=30°,则弦AB的长为( )
(2013•本溪)如图,⊙O的半径是3,点P是弦AB延长线上的一点,连接OP,若OP=4,∠APO=30°,则弦AB的长为( ) 如图,⊙O的半径OP=10cm,弦AB过OP的中点Q,且∠OQB=45°,则弦AB的长为
如图,⊙O的半径OP=10cm,弦AB过OP的中点Q,且∠OQB=45°,则弦AB的长为