Question

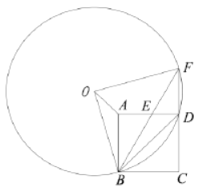
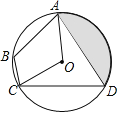
【题目】如图，已知⊙O的半径为2，四边形ABCD是⊙O的内接四边形，∠ABC＝∠AOC，且AD＝CD，则图中阴影部分的面积等于______．

Answer 1

【答案】π﹣

【解析】

根据题意可以得出三角形ACD是等边三角形，进而求出∠AOD，再根据直角三角形求出OE、AD，从而从扇形的面积减去三角形AOD的面积即可得出阴影部分的面积．

解：连接AC，OD，过点O作OE⊥AD，垂足为E，

∵∠ABC＝∠AOC，∠AOC＝2∠ADC，∠ABC+∠ADC＝180°，

∴∠ABC＝120°，∠ADC＝60°，

∵AD＝CD，

∴△ACD是正三角形，

∴∠AOD＝120°，OE＝2×cos60°＝1，AD＝2×sin60°×2＝2，

∴S阴影部分＝S扇形OAD﹣S△AOD＝×π×22﹣×2×1＝π﹣，

故答案为：π﹣．