题目内容
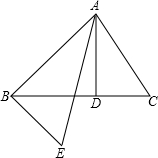 如图所示,AD是△ABC的高,∠EAB=∠DAC,EB⊥AB.
如图所示,AD是△ABC的高,∠EAB=∠DAC,EB⊥AB.
试证明:AD•AE=AC•AB.
证明:∵AD是△ABC的高,
∴AD⊥BC.
又∵EB⊥AB,
∴∠ADC=∠ABE=90°.
又∵∠EAB=∠DAC,
∴△ABE∽△ADC,
∴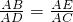 ,即AD•AE=AC•AB.
,即AD•AE=AC•AB.
分析:通过相似三角形(△ABE∽△ADC)的对应边成比例列出比例式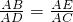 ,然后由比例的性质推得结论AD•AE=AC•AB.
,然后由比例的性质推得结论AD•AE=AC•AB.
点评:本题考查了相似三角形的判定与性质.解题中证明比例式通常都是通过相似三角形对应边成比例列出比例式,然后再把比例式转化为乘积式,也是常用的方法,需要熟练掌握并灵活运用.
∴AD⊥BC.
又∵EB⊥AB,
∴∠ADC=∠ABE=90°.
又∵∠EAB=∠DAC,
∴△ABE∽△ADC,
∴
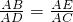 ,即AD•AE=AC•AB.
,即AD•AE=AC•AB.分析:通过相似三角形(△ABE∽△ADC)的对应边成比例列出比例式
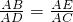 ,然后由比例的性质推得结论AD•AE=AC•AB.
,然后由比例的性质推得结论AD•AE=AC•AB.点评:本题考查了相似三角形的判定与性质.解题中证明比例式通常都是通过相似三角形对应边成比例列出比例式,然后再把比例式转化为乘积式,也是常用的方法,需要熟练掌握并灵活运用.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 如图所示,AD是△ABC中BC边上的中线,已知△ABC的面积为12,则△ACD的面积等于
如图所示,AD是△ABC中BC边上的中线,已知△ABC的面积为12,则△ACD的面积等于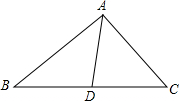 如图所示,AD是△ABC的中线,AB=6cm,AC=5cm,求△ABD和△ADC的周长的差.
如图所示,AD是△ABC的中线,AB=6cm,AC=5cm,求△ABD和△ADC的周长的差. 55、如图所示,AD是∠BAC的平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,且BD=CD.
55、如图所示,AD是∠BAC的平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,且BD=CD. 26、已知如图所示,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F,四边形AEDF是菱形吗?说明理由.
26、已知如图所示,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F,四边形AEDF是菱形吗?说明理由. 如图所示,AD是△ABC的高,AE是⊙O的直径,A,B,C三点都在圆上,∠DAC=30°,则∠BAE为( )
如图所示,AD是△ABC的高,AE是⊙O的直径,A,B,C三点都在圆上,∠DAC=30°,则∠BAE为( )