Question

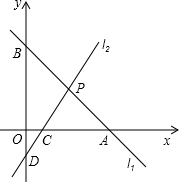如图，两个一次函数的图象分别是直线l₁和l₂，两直线与x轴、y轴的交点为A、B、C、D，且OB=2OD，l₁、l₂交于P（2，2），OB•OD=8，
求：（1）两函数的解析式；（2）S_△PAC：S_{四边形PCOB}．

Answer 1

分析：（1）由OB=2OD，OB•OD=8，可得B，D两点的坐标，又l₁、l₂交于P（2，2）已知，即可求出函数的解析式；
（2）先求出两图形面积，然后作比．

解答：解：（1）由OB=2OD，OB•OD=8，可得B，D两点的坐标分别为B（0，4），D（0，-2），
又已知P（2，2），
设直线l₁和l₂的方程分别为：y₁=k₁x+b₁，y₂=k₂x+b₂，
将B（0，4），D（0，-2），P（2，2）代入方程有

4=b1 2=2k1+b1

，

-2=b2 2=2k2+b2

，
解得：

k1=-1 b1=4

，

k2=2 b2=-2

，
∴两函数的解析式分别为：y=-x+4，y=2x-2；

（2）由上易知C（1，0），
∴S_△PAC=

1

2

×3×2=3，
S_{四边形PCOB}=S_△AOB-S_△PAC=

1

2

×4×4-3=5，
S_△PAC：S_{四边形PCOB}=3：5．

点评：本题考查了两条直线相交或平行问题，难度较大，做题须根据图形仔细分析．