题目内容
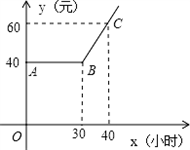
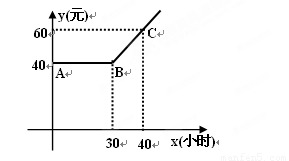
某市推出电脑上网包月制，每月收取费用y（元）与上网时间x（小时）的函数关系式如图所示，其中BA是线段，且BA∥x轴，AC是射线，若小李12月份上网费用为84元，则他在该月份上网时间是________小时．
38
分析：由图可知，当x≥30时，图象是一次函数图象，设函数关系式为y=kx+b，使用待定系数法求解即可，因为60＜84＜90，当y=84时，代入函数关系计算出x的值即可．
解答：当x≥30时，设函数关系式为y=kx+b，
则
，
解得
．
所以y=3x-30；
由84=3x-30
解得：x=38，所以他在该月份上网时间是38小时．
故答案为：38．
点评：本题考查了待定系数法求一次函数关系式，根据已知得出点的坐标进而求出解析式是解题关键．
分析：由图可知，当x≥30时，图象是一次函数图象，设函数关系式为y=kx+b，使用待定系数法求解即可，因为60＜84＜90，当y=84时，代入函数关系计算出x的值即可．
解答：当x≥30时，设函数关系式为y=kx+b，
则
，解得
．所以y=3x-30；
由84=3x-30
解得：x=38，所以他在该月份上网时间是38小时．
故答案为：38．
点评：本题考查了待定系数法求一次函数关系式，根据已知得出点的坐标进而求出解析式是解题关键．
练习册系列答案
相关题目
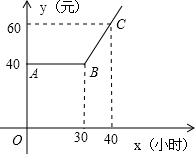
中BA是线段，且BA∥x轴，AC是射线．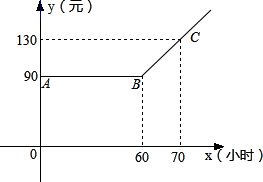
的关系如图所示，其中AB是线段，且AB∥x轴，BC是射线
