题目内容
（2013•日照）如图（a），有一张矩形纸片ABCD，其中AD=6cm，以AD为直径的半圆，正好与对边BC相切，将矩形纸片ABCD沿DE折叠，使点A落在BC上，如图（b）．则半圆还露在外面的部分（阴影部分）的面积为
（3π-
）cm2
9
| ||
| 4 |
（3π-
）cm2
．9
| ||
| 4 |
分析：如图，露在外面部分的面积可用扇形ODK与△ODK的面积差来求得，在Rt△A'DC中，可根据AD即圆的直径和CD即圆的半径长，求出∠DA'C的度数，进而得出∠ODH和∠DOK的度数，即可求得△ODK和扇形ODK的面积，由此可求得阴影部分的面积．
解答：解：作OH⊥DK于H，连接OK，
∵以AD为直径的半园，正好与对边BC相切，
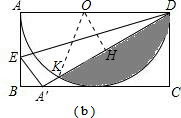
∴AD=2CD，
∴A'D=2CD，
∵∠C=90°，
∴∠DA'C=30°，
∴∠ODH=30°，
∴∠DOH=60°，
∴∠DOK=120°，
∴扇形ODK的面积为
=3πcm2，
∵∠ODH=∠OKH=30°，OD=3cm，
∴OH=
cm，DH=
cm；
∴DK=3
cm，
∴△ODK的面积为
cm2，
∴半圆还露在外面的部分（阴影部分）的面积是：（3π-
）cm2．
故答案为：（3π-
）cm2．
∵以AD为直径的半园，正好与对边BC相切，
∴AD=2CD，
∴A'D=2CD，
∵∠C=90°，
∴∠DA'C=30°，
∴∠ODH=30°，
∴∠DOH=60°，
∴∠DOK=120°，
∴扇形ODK的面积为
| 120π×32 |
| 360 |
∵∠ODH=∠OKH=30°，OD=3cm，
∴OH=
| 3 |
| 2 |
3
| ||
| 2 |
∴DK=3
| 3 |
∴△ODK的面积为
9
| ||
| 4 |
∴半圆还露在外面的部分（阴影部分）的面积是：（3π-
9
| ||
| 4 |
故答案为：（3π-
9
| ||
| 4 |
点评：此题考查了折叠问题，解题时要注意找到对应的等量关系；还考查了圆的切线的性质，垂直于过切点的半径；还考查了直角三角形的性质，直角三角形中，如果有一条直角边是斜边的一半，那么这条直角边所对的角是30度．
练习册系列答案
相关题目
（2013•日照）如图，在△ABC中，以BC为直径的圆分别交边AC、AB于D、E两点，连接BD、DE．若BD平分∠ABC，则下列结论不一定成立的是（ ）
（2013•日照）如图，H7N9病毒直径为30纳米（1纳米=10-9米），用科学记数法表示这个病毒直径的大小，正确的是（ ）
（2013•日照）如图是某学校全体教职工年龄的频数分布直方图（统计中采用“上限不在内”的原则，如年龄为36岁统计在36≤x＜38小组，而不在34≤x＜36小组），根据图形提供的信息，下列说法中错误的是（ ）
（2013•日照）如图，已知抛物线y1=-x2+4x和直线y2=2x．我们约定：当x任取一值时，x对应的函数值分别为y1、y2，若y1≠y2，取y1、y2中的较小值记为M；若y1=y2，记M=y1=y2．下列判断：
（2013•日照）如右图，直线AB交双曲线