Question

已知，在矩形ABCD中，AB=a，BC=b，动点M从点A出发沿边AD向点D运动．

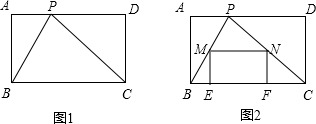
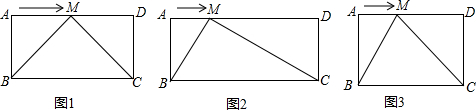
（1）如图1，当b=2a，点M运动到边AD的中点时，请证明∠BMC=90°；

（2）如图2，当b＞2a时，点M在运动的过程中，是否存在∠BMC=90°，若存在，请给与证明；若不存在，请说明理由；

（3）如图3，当b＜2a时，（2）中的结论是否仍然成立？请说明理由．

Answer 1

（1）证明：∵b=2a，点M是AD的中点，

∴AB=AM=MD=DC=a，

又∵在矩形ABCD中，∠A=∠D=90°，

∴∠AMB=∠DMC=45°，

∴∠BMC=90°．

（2）解：存在，

理由：若∠BMC=90°，

则∠AMB+∠DMC=90°，

又∵∠AMB+∠ABM=90°，

∴∠ABM=∠DMC，

又∵∠A=∠D=90°，

∴△ABM∽△DMC，

∴=，

设AM=x，则=，

整理得：x²﹣bx+a²=0，

∵b＞2a，a＞0，b＞0，

∴△=b²﹣4a²＞0，

∴方程有两个不相等的实数根，且两根均大于零，符合题意，

∴当b＞2a时，存在∠BMC=90°，

（3）解：不成立．

理由：若∠BMC=90°，

由（2）可知x²﹣bx+a²=0，

∵b＜2a，a＞0，b＞0，

∴△=b²﹣4a²＜0，

∴方程没有实数根，

∴当b＜2a时，不存在∠BMC=90°，即（2）中的结论不成立．