题目内容
如图,点A.B.C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.
(1)求证:AP是⊙O的切线;
(2)求PD的长.

考点:切线的判定;圆周角定理;解直角三角形。
解答:(1)证明:连接OA.
∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠ACP=∠CAO=30°,
∴∠AOP=60°,
∵AP=AC,
∴∠P=∠ACP=30°,
∴∠OAP=90°,
∴OA⊥AP,
∴AP是⊙O的切线,
(2)解:连接AD.
∵CD是⊙O的直径,
∴∠CAD=90°,
∴AD=AC•tan30°=3×![]() =
=![]() ,
,
∵∠ADC=∠B=60°,
∴∠PAD=∠ADC﹣∠P=60°﹣30°,
∴∠P=∠PAD,
∴PD=AD=![]() .
.


练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
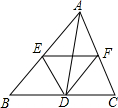
 如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )
如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )| A、EF与AD互相平分 | ||
B、EF=
| ||
| C、AD平分∠BAC | ||
| D、△DEF∽△ACB |
 如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )
如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )| A、AD平分∠BAC | ||
B、EF=
| ||
| C、EF与AD互相平分 | ||
| D、△DFE是△ABC的位似图形 |
 5、如图,点D、E、F分别是△ABC的边AB、BC、AC的中点,连接DE、EF,要使四边形ADEF为正方形,还需增加条件:
5、如图,点D、E、F分别是△ABC的边AB、BC、AC的中点,连接DE、EF,要使四边形ADEF为正方形,还需增加条件: 如图,点D,E,F分别是△ABC的三边AB,AC,BC上的中点,如果△ABC的面积是18cm2,则△DBF的面积是
如图,点D,E,F分别是△ABC的三边AB,AC,BC上的中点,如果△ABC的面积是18cm2,则△DBF的面积是 如图,点D、E、F分别是△ABC三边AB、BC、AC的中点,则△DEF的周长是△ABC周长的( )
如图,点D、E、F分别是△ABC三边AB、BC、AC的中点,则△DEF的周长是△ABC周长的( )