题目内容
 如图,C为线段AE上一动点(不与点A、E重合).在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于H,AD与BC交于P,BE与CD交于Q,连接PQ、CH.给出以下五个结论:①AD=BE,②PQ∥AE,③AP=BQ,④DE=DP,⑤∠AHB=60°,⑥HC平分∠AHE,⑦△CDP≌△CEQ.其中正确结论的个数是( )
如图,C为线段AE上一动点(不与点A、E重合).在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于H,AD与BC交于P,BE与CD交于Q,连接PQ、CH.给出以下五个结论:①AD=BE,②PQ∥AE,③AP=BQ,④DE=DP,⑤∠AHB=60°,⑥HC平分∠AHE,⑦△CDP≌△CEQ.其中正确结论的个数是( )| A、4个 | B、5个 | C、6个 | D、7个 |
分析:证明①可先证明△ACD≌△BCE,已有:AB=BC,CD=CE,易得∠ACD=∠BCE,其他的证明需要通过①得到,再利用三角形相似以及等边三角形的知识分别进行证明即可得出答案.
解答:解:①∵△ABC和△CDE为等边三角形
∴AC=BC,CD=CE,∠BCA=∠DCB=60°
∴∠ACD=∠BCE
∴△ACD≌△BCE
∴AD=BE,故①正确;
由(1)中的全等得∠CBE=∠DAC,进而可求证△CQB≌△CPA,
∴AP=BQ,故③正确;
又∵∠PCQ=60°可知△PCQ为等边三角形,
∴∠PQC=∠DCE=60°,
∴PQ∥AE②成立,
∵∠QCP=60°,∠DPC=∠BCA+∠PAC>60°,
∴PD≠CD,
∴DE≠DP,故④DE=DP错误;
∵等边△ABC、等边△DCE,
∴∠ACB=∠CED,即BC∥DE,
同理可证AB∥CD,
即可得△BAE∽△QCE,△APC∽△ADE,
∴
=
,
=
,
∵BA=CA,DE=CE,
∴CQ=CP,
又∵∠PCQ=180°-∠ACB-∠ECD=60°,
∴△PCQ为等边三角形,
∵PC=CQ,CD=CE,∠PCD=∠QCE,
∴△CDP≌△CEQ.故⑦△CDP≌△CEQ,正确;
∵BC∥DE,
∴∠CBE=∠BED,
∵∠CBE=∠DAE,
∴∠AHB=∠HAE+∠AEH=60°,故⑤正确;
同理可得出∠AHE=120°,∠HAC=∠HCD,
∴∠DCE=∠AHC=60°,
∴HC平分∠AHE,故⑥正确,
故正确的有①②③⑤⑥⑦共6个,
故选:C.
∴AC=BC,CD=CE,∠BCA=∠DCB=60°
∴∠ACD=∠BCE
∴△ACD≌△BCE
∴AD=BE,故①正确;
由(1)中的全等得∠CBE=∠DAC,进而可求证△CQB≌△CPA,

∴AP=BQ,故③正确;
又∵∠PCQ=60°可知△PCQ为等边三角形,
∴∠PQC=∠DCE=60°,
∴PQ∥AE②成立,
∵∠QCP=60°,∠DPC=∠BCA+∠PAC>60°,
∴PD≠CD,
∴DE≠DP,故④DE=DP错误;
∵等边△ABC、等边△DCE,
∴∠ACB=∠CED,即BC∥DE,
同理可证AB∥CD,
即可得△BAE∽△QCE,△APC∽△ADE,
∴
| PC |
| DE |
| AC |
| AE |
| CQ |
| AB |
| CE |
| AE |
∵BA=CA,DE=CE,
∴CQ=CP,
又∵∠PCQ=180°-∠ACB-∠ECD=60°,
∴△PCQ为等边三角形,
∵PC=CQ,CD=CE,∠PCD=∠QCE,
∴△CDP≌△CEQ.故⑦△CDP≌△CEQ,正确;
∵BC∥DE,
∴∠CBE=∠BED,
∵∠CBE=∠DAE,
∴∠AHB=∠HAE+∠AEH=60°,故⑤正确;
同理可得出∠AHE=120°,∠HAC=∠HCD,
∴∠DCE=∠AHC=60°,
∴HC平分∠AHE,故⑥正确,
故正确的有①②③⑤⑥⑦共6个,
故选:C.
点评:此题主要考查了等边三角形的性质及三角形全的判定与性质以及相似三角形的判定与性质;熟练应用三角形全等的证明是正确解答本题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
 24、如图,C为线段AE上一动点,(不与A,E重合),在AE同侧分别作等边三角形ABC和CDE.则以下结论:①AD=BE ②CP=CQ ③AP=BQ ④DE=DP ⑤PQ∥AE中正确的有
24、如图,C为线段AE上一动点,(不与A,E重合),在AE同侧分别作等边三角形ABC和CDE.则以下结论:①AD=BE ②CP=CQ ③AP=BQ ④DE=DP ⑤PQ∥AE中正确的有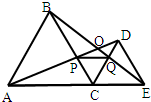 10、如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.其中正确的结论的个数是( )
10、如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.其中正确的结论的个数是( ) 15、如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°其中完全正确的是( )
15、如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°其中完全正确的是( ) 如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.
如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,连接PQ. 如图,C为线段AE上一动点(不与A,E重合)在AE同侧分别作等边△ABC和等边△CDE,AD与BE相交于点O,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.请你写出三个正确的结论:
如图,C为线段AE上一动点(不与A,E重合)在AE同侧分别作等边△ABC和等边△CDE,AD与BE相交于点O,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.请你写出三个正确的结论: