题目内容
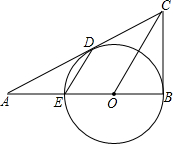
 已知:如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,∠AOD=∠APC.
已知:如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,∠AOD=∠APC.
(1)求证:AP是⊙O的切线;
(2)若AC=4CO,AP= ,求⊙O的半径.
,求⊙O的半径.
 (1)证明:连接OP;
(1)证明:连接OP;∵OP、OD是⊙O的半径,
∴OP=OD.
∴∠OPD=∠ODP(等边对等角).
∵PD⊥BE(已知),
∴∠OCD=90°.
∴∠ODP+∠AOD=90°.
∵∠AOD=∠APC,
∴∠OPD+∠APC=90°,即∠APO=90°.
∵OP是⊙O的半径,
∴AP是⊙O的切线;
(2)由(1)知,∠APO=90°,
则在Rt△APO中,AP2=AC•AO(射影定理).
∵AC=4CO,AP=
 ,
,∴(2
 )2=
)2= AO•AO,
AO•AO,∴AO=5.
∴OP=
 =
= ,即⊙O的半径是5.
,即⊙O的半径是5.分析:(1)连接OP.欲证OP是⊙O的切线,直需证明OP⊥AO.
(2)在Rt△APO中,利用射影定理即可求得AO的长度.然后利用勾股定理来求半径OP的长度.
点评:本题考查了切线的判定与性质、圆周角定理.解答(2)题时,也可以采用相似三角形的对应边成比例来求AO的长度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 交于A点.
交于A点.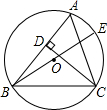 已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.
已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.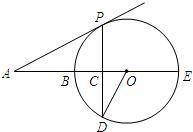 23、已知:如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,∠AOD=∠APC.
23、已知:如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,∠AOD=∠APC.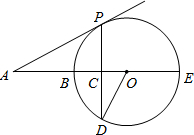 已知:如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,∠AOD=∠APC.
已知:如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,∠AOD=∠APC.