题目内容
 如图:已知?ABCD的对角线AC、BD相交于点O,EF过点O,且与BC、AD分别相交于E、F.求证:OE=OF.
如图:已知?ABCD的对角线AC、BD相交于点O,EF过点O,且与BC、AD分别相交于E、F.求证:OE=OF.
证明:
证法一:∵?ABCD
∴AD∥BC,OA=OC,
∴∠FAC=∠ACB(或∠AFO=∠CEO),
又∵∠AOF=∠COE,
在△AOF和△COE中,
 ,
,
∴△AOF≌△COE,
∴OE=OF;
证法二:∵?ABCD
∴AD∥BC,OA=OC,
∴ ,
,
∴OE=OF.
分析:证法一利用?ABCD的性质得到AD∥BC,OA=OC,且∠AOF=∠ACB(或∠AFO=∠CEO),又∠AOF=∠COE,然后利用全等三角形的判定方法即可证明△AOF≌△COE,再利用全等三角形的性质即可证明结论;
证法二由?ABCD可以得到AD∥BC,OA=OC,然后利用平行线分线段成比例即可证明结论.
点评:此题把全等三角形放在平行四边形的背景中,利用平行四边形的性质来证明三角形全等,最后利用全等三角形的性质解决问题.
证法一:∵?ABCD
∴AD∥BC,OA=OC,
∴∠FAC=∠ACB(或∠AFO=∠CEO),
又∵∠AOF=∠COE,
在△AOF和△COE中,
 ,
,∴△AOF≌△COE,
∴OE=OF;
证法二:∵?ABCD
∴AD∥BC,OA=OC,
∴
 ,
,∴OE=OF.
分析:证法一利用?ABCD的性质得到AD∥BC,OA=OC,且∠AOF=∠ACB(或∠AFO=∠CEO),又∠AOF=∠COE,然后利用全等三角形的判定方法即可证明△AOF≌△COE,再利用全等三角形的性质即可证明结论;
证法二由?ABCD可以得到AD∥BC,OA=OC,然后利用平行线分线段成比例即可证明结论.
点评:此题把全等三角形放在平行四边形的背景中,利用平行四边形的性质来证明三角形全等,最后利用全等三角形的性质解决问题.

练习册系列答案
相关题目
 14、如图,已知?ABCD中,AB=4,BC=6,BC边上的高AE=2,则DC边上的高AF的长是
14、如图,已知?ABCD中,AB=4,BC=6,BC边上的高AE=2,则DC边上的高AF的长是

 26、如图,已知?ABCD,AE平分∠BAD,交DC于E,DF⊥BC于F,交AE于G,且DF=AD.
26、如图,已知?ABCD,AE平分∠BAD,交DC于E,DF⊥BC于F,交AE于G,且DF=AD.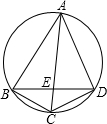 如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于
如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于 如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.
如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.