Question

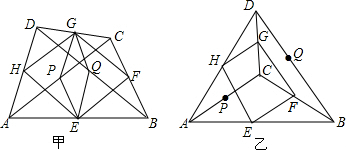
4．如图甲，已知任意四边形ABCD，且线段AB，BC，CD，DA，AC，BD的中点分别是E，F，G，H，P，Q，顺次连接EF，FG，GH，HE，得到四边形EFGH，顺次连接EQ，QG，GP，PE，得到四边形PEQG．
（1）判断四边形EFGH，PEQG的形状，并证明；
（2）若四边形ABCD如图乙所示，请你判断（1）中的两个结论是否成立．

Answer 1

分析 （1）根据三角形的中位线定理，得GH∥EF∥AC，GH=EF=$\frac{1}{2}$AC，所以得到的是平行四边形；根据三角形的中位线定理，得GP∥EQ∥AD，GP=EQ=$\frac{1}{2}$AD，所以得到的是平行四边形．
（2）类似于（1）中的2个结论都成立：根据三角形的中位线定理，得GH∥EF∥AC，GH=EF=$\frac{1}{2}$AC，所以得到的是平行四边形；根据三角形的中位线定理，得GP∥EQ∥AD，GP=EQ=$\frac{1}{2}$AD，所以得到的是平行四边形．

解答 解：（1）四边形EFGH是平行四边形．理由如下：
∵E、F分别是AB、BC的中点，
∴EF∥AC，EF=$\frac{1}{2}$AC．
同理，得HG∥AC，HG=$\frac{1}{2}$AC，
∴EF∥HG，EF=HG，
∴四边形EFGH是平行四边形．

四边形PEQG是平行四边形．理由如下：
∵G、P分别是CD、AC的中点，
∴GP∥AD，GP=$\frac{1}{2}$AD．
同理，得QE∥AD，QE=$\frac{1}{2}$AD，
∴GP∥QE，GP=QE，
∴四边形PEQG是平行四边形．

（2）（1）中的两个结论都成立．
四边形EFGH是平行四边形．理由如下：
∵E、F分别是AB、BC的中点，
∴EF∥AC，EF=$\frac{1}{2}$AC．
同理，得HG∥AC，HG=$\frac{1}{2}$AC，
∴EF∥HG，EF=HG，
∴四边形EFGH是平行四边形．
如图乙，顺次连接EQ，QG，GP，PE，得到四边形PEQG．
四边形PEQG是平行四边形．理由如下：
∵G、P分别是CD、AC的中点，
∴GP∥AD，GP=$\frac{1}{2}$AD．
同理，得QE∥AD，QE=$\frac{1}{2}$AD，
∴GP∥QE，GP=QE，
∴四边形PEQG是平行四边形．

点评 主要考查了平行四边形的判定和三角形的中位线定理．
数量关系：三角形的中位线等于第三边一半．位置关系：三角形中位线平行于第三边．
总结：顺次连接四边形各边中点所得四边形是平行四边形．