题目内容
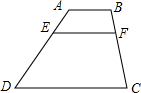
如图，AB∥EF∥CD，已知AB=20，CD=80，BC=100，那么EF的值是（ ）| A、10 | B、12 | C、16 | D、18 |
分析：先由AB∥CD，得△EAB∽△ECD，而AB=20，CD=80，所以
=
=
；又EF∥CD，得到
=
=
，即可得到EF的值．
| BE |
| ED |
| 20 |
| 80 |
| 1 |
| 4 |
| EF |
| CD |
| BE |
| BD |
| 1 |
| 5 |
解答：解：∵AB∥CD，
∴△EAB∽△ECD，
∴
=
，
而AB=20，CD=80，
∴
=
=
，
∴
=
；
又∵EF∥CD，
∴
=
=
，
而CD=80，
∴EF=
=16．
故选C．
∴△EAB∽△ECD，
∴
| BE |
| ED |
| AB |
| CD |
而AB=20，CD=80，
∴
| BE |
| ED |
| 20 |
| 80 |
| 1 |
| 4 |
∴
| BE |
| BD |
| 1 |
| 5 |
又∵EF∥CD，
∴
| EF |
| CD |
| BE |
| BD |
| 1 |
| 5 |
而CD=80，
∴EF=
| 80 |
| 5 |
故选C．
点评：本题考查了相似三角形的判定与性质．平行于三角形一边的直线与三角形两边相交，所得的三角形与原三角形相似．
练习册系列答案
名校课堂系列答案
相关题目
如图，AB∥EF∥CD，AB=2，CD=8，AE：ED=1：5，则EF的长度为
如图，AB∥EF，∠B=46°，∠F=54°，则∠BCF=
已知一角的两边与另一个角的两边平行，结合图形，试探索这两个角之间的数量关系．
如图，AB⊥EF，CD⊥EF且AB=CD，则图中全等三角形有
已知：如图，AB∥EF，BC⊥CD，则∠α、∠β、∠γ之间的关系是（ ）