题目内容
(2013•海沧区一模)(1)计算:
÷(
)-1+(-1)2013×40;
(2)因式分解:x3-2x2y+xy2,并计算x=2012,y=2013时,此式子的值.
(3)在直角三角形ABC中,∠C=90°,AB=10,AC=8,求cos∠B的值.
| 4 |
| 1 |
| 2 |
(2)因式分解:x3-2x2y+xy2,并计算x=2012,y=2013时,此式子的值.
(3)在直角三角形ABC中,∠C=90°,AB=10,AC=8,求cos∠B的值.
分析:(1)先计算指数幂,然后计算乘除法,最后计算加减法;
(2)先提取公因式x,然后利用完全平方公式进行因式分解,再代入求值;
(3)首先由勾股定理求得BC=6,然后根据余弦三角函数定义进行解答.
(2)先提取公因式x,然后利用完全平方公式进行因式分解,再代入求值;
(3)首先由勾股定理求得BC=6,然后根据余弦三角函数定义进行解答.
解答:解:(1)原式=2÷2+(-1)×1
=1-1
=0;
(2)原式=x(x2-2xy+y2)
=x(x-y)2,
当x=2012,y=2013时,x(x-y)2=2012×(-1)2=2012;
(3)∵在直角三角形ABC中,∠C=90°,
∴AC2+BC2=AB2,
∵AB=10,AC=8,
∴BC=
-
=6,
∵cos∠B=
=
,
∴cos∠B=
.
=1-1
=0;
(2)原式=x(x2-2xy+y2)
=x(x-y)2,
当x=2012,y=2013时,x(x-y)2=2012×(-1)2=2012;
(3)∵在直角三角形ABC中,∠C=90°,
∴AC2+BC2=AB2,
∵AB=10,AC=8,
∴BC=
| AB2-AC2 |
| 102-82 |
∵cos∠B=
| BC |
| AB |
| 6 |
| 10 |
∴cos∠B=
| 3 |
| 5 |
点评:本题考查了锐角三角函数的定义、零指数幂、负整数指数幂以及因式分解等知识点.难度不大,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
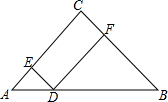 (2013•海沧区一模)如图,在等腰直角三角形ABC中,AC=BC=2,D为AB上的动点(不与A,B重合),过D作DE⊥AC于E,DF⊥BC于F,设AD的长度为x,DE与DF的长度和为y.则能表示y与x之间的函数关系的图象大致是( )
(2013•海沧区一模)如图,在等腰直角三角形ABC中,AC=BC=2,D为AB上的动点(不与A,B重合),过D作DE⊥AC于E,DF⊥BC于F,设AD的长度为x,DE与DF的长度和为y.则能表示y与x之间的函数关系的图象大致是( )