题目内容
 21、推理填空:如图:
21、推理填空:如图:①若∠1=∠2,
则
AB
∥CD
(内错角相等,两直线平行);若∠DAB+∠ABC=180°,
则
AD
∥BC
(同旁内角互补,两直线平行);②当
AB
∥CD
时,∠C+∠ABC=180°(两直线平行,同旁内角互补);
③当
AD
∥BC
时,∠3=∠C (两直线平行,内错角相等).
分析:根据平行线的性质和平行线的判定直接完成填空.两条直线平行,则同位角相等,内错角相等,同旁内角互补;反之亦成立.
解答:解:①若∠1=∠2,
则AB∥CD(内错角相等,两条直线平行);
若∠DAB+∠ABC=180°,
则AD∥BC(同旁内角互补,两条直线平行);
②当AB∥CD时,
∠C+∠ABC=180°(两条直线平行,同旁内角互补);
③当AD∥BC时,
∠3=∠C (两条直线平行,内错角相等).
则AB∥CD(内错角相等,两条直线平行);
若∠DAB+∠ABC=180°,
则AD∥BC(同旁内角互补,两条直线平行);
②当AB∥CD时,
∠C+∠ABC=180°(两条直线平行,同旁内角互补);
③当AD∥BC时,
∠3=∠C (两条直线平行,内错角相等).
点评:在做此类题的时候,一定要细心观察,看两个角到底是哪两条直线被第三条直线所截而形成的角.

练习册系列答案
相关题目
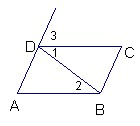 17、推理填空:如图:
17、推理填空:如图: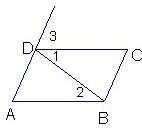 18、推理填空:
18、推理填空: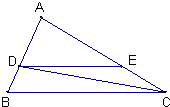
 17、推理填空:
17、推理填空: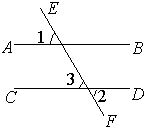 25、完成推理填空:如图:直线AB、CD被EF所截,若已知AB∥CD,
25、完成推理填空:如图:直线AB、CD被EF所截,若已知AB∥CD,