题目内容
(2002•聊城)如图,A、B、C、D是圆周上的四个点, ,且弦AB=8,弦CD=4,则图中两个弓形(阴影)的面积和是 (结果保留三个有效数字).
,且弦AB=8,弦CD=4,则图中两个弓形(阴影)的面积和是 (结果保留三个有效数字).
【答案】分析:易得弧AB,CD是一个半圆弧,我们将C点转到与A点重合处,那么O、B、D′就在一条直线上,而且是一直径,所以阴影部分的面积=半圆的面积-一个直角三角形的面积,然后依面积公式计算即可.
解答:
解:∵ ,
,
∴弧AB,CD就是一个半圆弧,
则B、O、D′就在一条直线上,而且BD′是一直径,
∴∠D′AB=90°,弧AD′=弧CD,
∴AD′=CD=4,
在Rt△CAB中,由勾股定理得:BD′= =4
=4 ,
,
∴OB=2 ,
,
∴阴影部分的面积= S⊙O-S△D′AB
S⊙O-S△D′AB
=π×(2 )2×
)2× -
- ×4×8
×4×8
=15.4.
点评:本题的关键是作辅助线,从图中看出阴影部分的面积=半圆的面积-一个直角三角形的面积.
解答:

解:∵
 ,
,∴弧AB,CD就是一个半圆弧,
则B、O、D′就在一条直线上,而且BD′是一直径,
∴∠D′AB=90°,弧AD′=弧CD,
∴AD′=CD=4,
在Rt△CAB中,由勾股定理得:BD′=
 =4
=4 ,
,∴OB=2
 ,
,∴阴影部分的面积=
 S⊙O-S△D′AB
S⊙O-S△D′AB=π×(2
 )2×
)2× -
- ×4×8
×4×8=15.4.
点评:本题的关键是作辅助线,从图中看出阴影部分的面积=半圆的面积-一个直角三角形的面积.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 x2+bx+c和x轴正半轴相交于A、B两点,AB=4,P为抛物线上的一点,它的横坐标为9,∠PBO=135°,cot∠PAB=
x2+bx+c和x轴正半轴相交于A、B两点,AB=4,P为抛物线上的一点,它的横坐标为9,∠PBO=135°,cot∠PAB= .
.
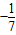 x2+bx+c和x轴正半轴相交于A、B两点,AB=4,P为抛物线上的一点,它的横坐标为9,∠PBO=135°,cot∠PAB=
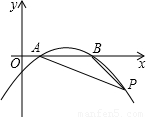
x2+bx+c和x轴正半轴相交于A、B两点,AB=4,P为抛物线上的一点,它的横坐标为9,∠PBO=135°,cot∠PAB= .
.

 ,且弦AB=8,弦CD=4,则图中两个弓形(阴影)的面积和是 (结果保留三个有效数字).
,且弦AB=8,弦CD=4,则图中两个弓形(阴影)的面积和是 (结果保留三个有效数字).