题目内容
如图△ABC中,AB=AC=5,BC=6,D、E分别是边AB、AC上的两个动点(D不与A、B重合),且保持DE∥BC,以ED为边,在点A的异侧作正方形DEFG.
(1)试求△ABC的面积;
(2)当边FG与BC重合时,求正方形DEFG的边长;
(3)设AD=x,当△BDG是等腰三角形时,求出AD的长.
(1)12;(2)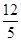 ;(3)AD=
;(3)AD=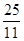 或
或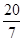 或
或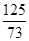 .
.
解析试题分析:(1)过A作AH⊥BC于H,根据等腰三角形三线合一的性质可得BH的长,再根据勾股定理可求得AH的长,最后根据三角形的面积公式求解即可;
(2)设此时正方形的边长为a,由DE∥BC可得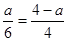 ,即可求得结果;
,即可求得结果;
(3)先根据相似三角形的性质表示出DE的长,再分当BD=DG时,当BD=BG时,当BG=DG时,三种情况根据相似三角形的性质求解即可.
(1)过A作AH⊥BC于H,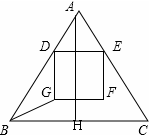
∵AB=AC=5,BC=6,
∴BH=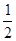 BC=3,
BC=3,
∵AH2=AB2-BH2
∴AH=4
∴S△ABC=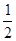 BC•AH=
BC•AH=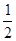 ×6×4=12;
×6×4=12;
(2)设此时正方形的边长为a,
∵DE∥BC,
∴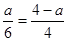 ,解得a=
,解得a=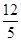 ;
;
(3)当AD=x时,由△ADE∽△ABC得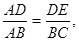
即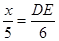 ,解得DE=
,解得DE=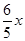 ,
,
当BD=DG时,5-x=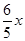 ,解得x=
,解得x=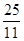 ,
,
当BD=BG时,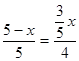 ,解得x=
,解得x=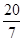 ,
,
当BG=DG时,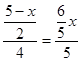 ,解得x=
,解得x=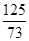 ,
,
∴当△BDG是等腰三角形时,AD=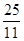 或
或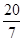 或
或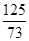 .
.
考点:动点问题的综合题
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
相关题目
 13、如图△ABC中,AB=AC,BD平分∠ABC,且△ABC∽△BDC,则∠A=
13、如图△ABC中,AB=AC,BD平分∠ABC,且△ABC∽△BDC,则∠A= 8、如图△ABC中,AB=3,AC=2,BO平分∠ABC,CO平分∠ACB.DE过点O交AB于D,交AC于E,且DE∥BC.则△ADE周长为
8、如图△ABC中,AB=3,AC=2,BO平分∠ABC,CO平分∠ACB.DE过点O交AB于D,交AC于E,且DE∥BC.则△ADE周长为 如图△ABC中,AB=AC,M是BC中点,D,E分别在AB,AC上,且BD=CE,求证:ME=MD.
如图△ABC中,AB=AC,M是BC中点,D,E分别在AB,AC上,且BD=CE,求证:ME=MD. 已知:如图△ABC中,AB=AC,AD和BE是高,它们交于点H,且AE=BE,
已知:如图△ABC中,AB=AC,AD和BE是高,它们交于点H,且AE=BE, 如图△ABC中,AB=6,AC=
如图△ABC中,AB=6,AC=