Question

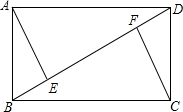（2012•思明区质检）如图，矩形ABCD，AE，CF分别垂直对角线BD于E，F．
（1）求证：△ABE≌△CDF；
（2）若∠ABD=60°，AB=1，求矩形ABCD的面积．

Answer 1

分析：（1）根据矩形的对边平行且相等可得AB=CD，AB∥CD，再根据两直线平行，内错角相等可得∠ABE=∠CDF，然后利用“角角边”证明即可；
（2）解直角三角形求出AD的长度，然后根据矩形的面积公式列式计算即可得解．

解答：（1）证明：∵四边形ABCD是矩形，
∴AB=CD，AB∥CD，
∴∠ABE=∠CDF，
∵AE⊥BD，CF⊥BD，
∴∠AEB=∠CFD=90°，
在△ABE和△CDF中，

∠ABE=∠CDF ∠AEB=∠CFD=90° AB=CD

，
∴△ABE≌△CDF（AAS）；

（2）解：∵四边形ABCD是矩形，
∴△BAD为直角三角形（或∠BAD=90°），
在Rt△BAD中，AB=1，∠ABD=60°，tan∠ABD=

AD

AB

，
∴AD=AB•tan60°=

3

，
∴S_矩形ABCD=AB•AD=1•

3

=

3

．

点评：本题考查了矩形的对边平行且相等的性质，全等三角形的判定，解直角三角形，是基础题，难度不大，熟记性质与判定方法是解题的关键．