题目内容
在△ABC中，若AC：BC：AB=7：24：25，则sinA=
- A.
- B.
- C.
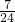
- D.
A
分析：先根据三角形的三边长判断出三角形的形状，再根据锐角三角函数的定义求解即可．
解答：∵△ABC中，AC：BC；AB=7：24：25，即72+242=252，
∴△ABC是直角三角形，∠C=90°．
sinA=
=．
故选A．
点评：本题考查了直角三角形的判定定理及锐角三角函数的定义，属较简单题目．
分析：先根据三角形的三边长判断出三角形的形状，再根据锐角三角函数的定义求解即可．
解答：∵△ABC中，AC：BC；AB=7：24：25，即72+242=252，
∴△ABC是直角三角形，∠C=90°．
sinA=
=．故选A．
点评：本题考查了直角三角形的判定定理及锐角三角函数的定义，属较简单题目．
练习册系列答案
阅读快车系列答案
相关题目