题目内容
 如图,将半径为4cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长度为
如图,将半径为4cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长度为
- A.4cm
- B.
 cm
cm - C.(2+
 )cm
)cm - D.
 cm
cm
B
分析:连接AO,过O作OD⊥AB,交 于点D,交弦AB于点E,根据折叠的性质可知OE=DE,再根据垂径定理可知AE=BE,在Rt△AOE中利用勾股定理即可求出AE的长,进而可求出AB的长.
于点D,交弦AB于点E,根据折叠的性质可知OE=DE,再根据垂径定理可知AE=BE,在Rt△AOE中利用勾股定理即可求出AE的长,进而可求出AB的长.
解答: 解:如图所示,
解:如图所示,
连接AO,过O作OD⊥AB,交 于点D,交弦AB于点E,
于点D,交弦AB于点E,
∵ 折叠后恰好经过圆心,
折叠后恰好经过圆心,
∴OE=DE,
∵⊙O的半径为4,
∴OE= OD=
OD= ×4=2,
×4=2,
∵OD⊥AB,
∴AE= AB,
AB,
在Rt△AOE中,
AE= =
= =2
=2 .
.
∴AB=2AE=4 .
.
故选B.
点评:本题考查的是垂径定理在实际生活中的运用及翻折变换的性质,根据题意画出图形,作出辅助线利用数形结合解答.
分析:连接AO,过O作OD⊥AB,交
 于点D,交弦AB于点E,根据折叠的性质可知OE=DE,再根据垂径定理可知AE=BE,在Rt△AOE中利用勾股定理即可求出AE的长,进而可求出AB的长.
于点D,交弦AB于点E,根据折叠的性质可知OE=DE,再根据垂径定理可知AE=BE,在Rt△AOE中利用勾股定理即可求出AE的长,进而可求出AB的长.解答:
 解:如图所示,
解:如图所示,连接AO,过O作OD⊥AB,交
 于点D,交弦AB于点E,
于点D,交弦AB于点E,∵
 折叠后恰好经过圆心,
折叠后恰好经过圆心,∴OE=DE,
∵⊙O的半径为4,
∴OE=
 OD=
OD= ×4=2,
×4=2,∵OD⊥AB,
∴AE=
 AB,
AB,在Rt△AOE中,
AE=
 =
= =2
=2 .
.∴AB=2AE=4
 .
.故选B.
点评:本题考查的是垂径定理在实际生活中的运用及翻折变换的性质,根据题意画出图形,作出辅助线利用数形结合解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
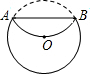 如图,将半径为4cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长度为( )
如图,将半径为4cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长度为( )| A、4cm | ||
B、4
| ||
C、(2+4
| ||
D、2
|
如图,将半径为4cm的圆形纸片折叠后,圆弧恰好经
过圆心O ,则折痕AB的长度为( )

过圆心O ,则折痕AB的长度为( )

| A.4 cm | B. cm cm | C.(2 + )cm )cm | D. cm cm |
 如图,将半径为4cm的圆形纸片折叠后,弧AB恰好经过圆心O,求折痕
如图,将半径为4cm的圆形纸片折叠后,弧AB恰好经过圆心O,求折痕
 如图,将半径为4cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长度为( )
如图,将半径为4cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长度为( )