题目内容
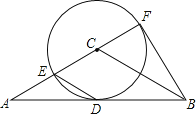
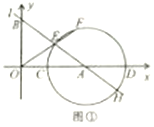
【题目】如图①,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是线段
是线段![]() 上一动点
上一动点![]() 以点
以点![]() 为圆心,
为圆心,![]() 长为半径作
长为半径作![]() 交
交![]() 轴于点
轴于点![]() ,分别交直线
,分别交直线![]() 于点
于点![]() 和点
和点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() .
.
(1)求直线![]() 的函数解析式和点
的函数解析式和点![]() 的坐标;
的坐标;
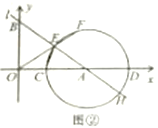
(2)如图②,连接![]() ,当
,当![]() 时,求证:
时,求证:![]() 并求点
并求点![]() 的坐标;
的坐标;
(3)当点![]() 在线段
在线段![]() 上运动时,求
上运动时,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;
;![]() ;(2)证明见解析;
;(2)证明见解析;![]() ;(3)
;(3)![]() 最大值为
最大值为![]() .
.
【解析】
(1)利用待定系数法求出b即可得出直线l表达式,即可得出结论;
(2)①先判断出∠CDF=2∠CDE,进而得出∠OAE=∠ODF,即可得出结论;
②设出EM=3m,AM=4m,进而得出点E坐标,即可得出OE的平方,再根据①的相似得出比例式得出OE的平方,建立方程即可得出结论;
(3)利用面积法求出OG,进而得出AG,HE,再构造相似三角形,即可得出结论.
解:(1)∵直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴直线![]() 的函数解析式
的函数解析式![]() ,
,
∴![]() ,
,
(2)①如图2,连接![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵四边形![]() 是
是![]() 的圆内接四边形,
的圆内接四边形,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
②过点![]() 作
作![]() 于
于![]() ,
,
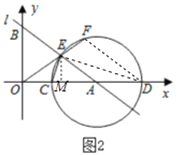
由①知,![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
由①知,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() (舍)或
(舍)或![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
(3)如图,设![]() 的半径为
的半径为![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,
,
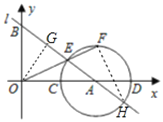
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
连接![]() ,
,
∵![]() 是
是![]() 直径,
直径,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 时,
时,![]() 最大值为
最大值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】官渡区某校八年级(1)班同学为了解某市2019年![]() 小区家庭月均用水情况,随机调查了该小区都分家庭,并将调查数据进行如下整理:
小区家庭月均用水情况,随机调查了该小区都分家庭,并将调查数据进行如下整理:
月均用水量 | 频数(户) | 频率 |
| 6 | 0.12 |
|
| 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 |
|
| 2 | 0.04 |
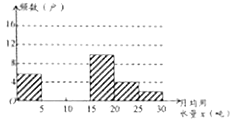
请解答下列问题:
(1)填空:样本容量是______,![]() ______,
______,![]() _______;
_______;
(2)把频数分布直方图补充完整;
(3)若该小区有1000户家庭,请估计该小区月均用水量满足![]() 的家庭有多少户?
的家庭有多少户?
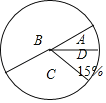
【题目】某市将开展演讲比赛活动,某校对参加选拔的学生的成绩按A、B、C、D四个等级进行统计,绘制了如下不完整的统计表和扇形统计图,
成绩等级 | 频数 | 频率 |
A | 4 | n |
B | m | 0.51 |
C | ||
D | 15 |
(1)求m、n的值;
(2)求“C等级”所对应的扇形圆心角的度数;
(3)已知成绩等级为A的4名学生中有1名男生和3名女生,现从中随机挑选2名学生代表学校参加全市比赛,求出恰好选中一男生和一女生的概率
【题目】“倡导全民阅读”“推动国民素质和社会文明程度显著提高”已成为“十三五”时期的重要工作.某中学在全校学生中随机抽取了部分学生对2018年度阅读情况进行问卷调查,并将收集的数据统计如表
数量/本 | 15 | 11 | 8 | 4 | 3 | 2 |
人数 | 80 | 60 | 50 | 100 | 40 | 70 |
根据表中的信息判断,下列结论错误的是( )
A. 该校参与调查的学生人数为400人
B. 该校学生2018年度阅读书数量的中位数为4本
C. 该校学生2018年度阅读书数量的众数为4本
D. 该校学生2018年平均每人阅读8本书