题目内容
已知非负数x,y,z满足 ,则w=3x+4y+5z的最大值是________;最小值是________.
,则w=3x+4y+5z的最大值是________;最小值是________.
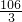 19
19分析:先设
 =t,用t表示出x、y、z的值,再由x,y,z为非负数即可求出t的取值范围,把所求代数式用t的形式表示出来,根据t的取值范围即可求解.
=t,用t表示出x、y、z的值,再由x,y,z为非负数即可求出t的取值范围,把所求代数式用t的形式表示出来,根据t的取值范围即可求解.解答:设
 =t,
=t,则x=2t+1,y=2-3t,z=4t+3,
∵x≥0;y≥0;z≥0,
∴2t+1≥0;2-3t≥0;4t+3≥0;
解得t≥-
 ;t≤
;t≤ ; t≥-
; t≥- ;
;∴-
 ≤t≤
≤t≤ ,
,∵w=3x+4y+5Z,把x=2t+1,y=2-3t,z=4t+3,代入得:w=14t+26
∴t=
 ,
,∴-
 ≤
≤ ≤
≤ ,
,解得,19≤w≤
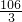 .
.∴w的最大值是
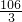 ;最小值是19.
;最小值是19.故答案为:
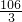 ;19.
;19.点评:本题考查的是一次函数的性质,通过设参数的方法求出W的取值范围是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目