题目内容
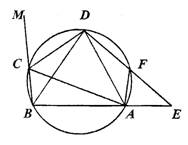
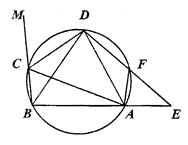
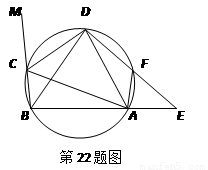
(本题满分8分)在圆内接四边形ABCD中,CD为∠BCA外角的平分线,F为上一点,BC=AF,延长DF与BA的延长线交于E.
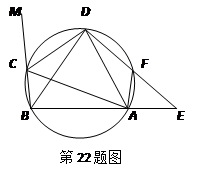 (1)求证△ABD为等腰三角形.
(1)求证△ABD为等腰三角形.
(2)求证AC•AF=DF•FE.
(1)证法一:连CF、BF
∠ACD=∠MCD=∠CDB+∠CBD=∠CFB+∠CFD=∠DFB
而∠ACD=∠DFB=∠DAB又∠ACD=∠DBA
∴∠DAB=∠DBA ∴△ABD为等腰三角形 ……(3分)
证法二:
由题意有∠MCD=∠ACD =∠DBA,又∠MCD+∠BCD=∠DAB+∠BCD=180°,
∴∠MCD=∠DAB,∴∠DAB=∠DBA即△.ABD为等腰三角形 ……(3分)
(2)由(1)知AD=BD,BC=AF,则弧AFD=弧BCD,弧AF=弧BC,
∴弧CD=弧DF,∴弧CD=弧DF……① ……(4分)
又BC=AF,∴∠BDC=∠ADF,∠BDC+∠BDA=∠ADF+∠BDA,即∠CDA=∠BDF,
而∠FAE+∠BAF=∠BDF+∠BAF=180°,∴∠FAE=∠BDF=∠CDA,
同理∠DCA=∠AFE ……(6分)
∴在△CDA与△FDE中,∠CDA=∠FAE,∠DCA=∠AFE
∴△CDA∽△FAE
∴ ,即CD·EF=AC·AF,又由①有AC·AF=DF·EF
命题即证 ……(8分)
解析:略

练习册系列答案
相关题目
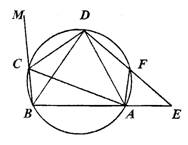
 (1)求证△ABD为等腰三角形.
(1)求证△ABD为等腰三角形.