题目内容
 (1)如图,AB、CD相交于O点,∠AOC=(2x-10)°,∠DOB=(x+25)°,求∠AOD的度数.
(1)如图,AB、CD相交于O点,∠AOC=(2x-10)°,∠DOB=(x+25)°,求∠AOD的度数.
(2)解方程: .
.
解:(1)∵∠AOC=(2x-10)°,∠DOB=(x+25)°,∠AOC=∠BOD,
∴2x-10=x+25,
∴x=35,
∴∠AOC=60°,
∴∠AOD=180°-60°=120°,
答:∠AOD的度数是120°.
(2)方程两边都乘以6得:2(2x+1)-(10x+1)=6,
去括号得:4x+2-10x-1=6,
移项得:4x-10x=6-2+1,
合并同类项得:-6x=5,
系数化成1得:x=- .
.
分析:(1)根据对顶角相等得出2x-10=x+25,求出x,求出∠AOC,即可求出∠AOD;
(2)方程两边都乘以6、去括号得到4x+2-10x-1=6移项、合并同类项得出-6x=5,方程的两边都除以-6即可得出答案.
点评:本题考查了对顶角、邻补角、解一元一次方程,等式的性质的应用,注意:对顶角相等,邻补角互补,方程两边都乘以6得出2(2x+1)-(10x+1)=6,而不是2(2x+1)-10x+1=1.
∴2x-10=x+25,
∴x=35,
∴∠AOC=60°,
∴∠AOD=180°-60°=120°,
答:∠AOD的度数是120°.
(2)方程两边都乘以6得:2(2x+1)-(10x+1)=6,
去括号得:4x+2-10x-1=6,
移项得:4x-10x=6-2+1,
合并同类项得:-6x=5,
系数化成1得:x=-
 .
.分析:(1)根据对顶角相等得出2x-10=x+25,求出x,求出∠AOC,即可求出∠AOD;
(2)方程两边都乘以6、去括号得到4x+2-10x-1=6移项、合并同类项得出-6x=5,方程的两边都除以-6即可得出答案.
点评:本题考查了对顶角、邻补角、解一元一次方程,等式的性质的应用,注意:对顶角相等,邻补角互补,方程两边都乘以6得出2(2x+1)-(10x+1)=6,而不是2(2x+1)-10x+1=1.

练习册系列答案
相关题目
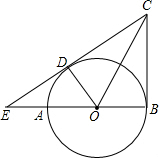 如图,AB是⊙O的直径,CB、CE分别切⊙O于点B、D,CE与BA的延长线交于点E,连接OC、OD.
如图,AB是⊙O的直径,CB、CE分别切⊙O于点B、D,CE与BA的延长线交于点E,连接OC、OD.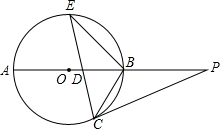 PA上截取PD=PC,连接CD,并延长交⊙O于点E.
PA上截取PD=PC,连接CD,并延长交⊙O于点E.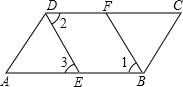
 19、如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.其中正确的结论是( )
19、如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.其中正确的结论是( ) 如图,AB、CD相交于点O,试添加一个条件使得△AOD∽△COB,你添加的条件是
如图,AB、CD相交于点O,试添加一个条件使得△AOD∽△COB,你添加的条件是