题目内容
 已知半径为5的⊙P与轴交于点M(0,-4),N(0,-10),则点P的坐标为________.
已知半径为5的⊙P与轴交于点M(0,-4),N(0,-10),则点P的坐标为________.
(4,-7),(-4,-7)
分析:设点P的横坐标是x,过P作PE⊥MN,则点P在MN的垂直平分线上,点P的横坐标是-7,设点P的横坐标是x,在Rt△MPE中,根据勾股定理得:MP2=ME2+PE2,故可求得PE的长.
解答: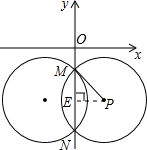 解:点P在MN的垂直平分线上,点M(0,-4),N(0,-10),
解:点P在MN的垂直平分线上,点M(0,-4),N(0,-10),
∴点P的纵坐标是-7,
设点P的横坐标是x,过P作PE⊥MN,
在△MPE中根据勾股定理得到MP2=ME2+PE2,
即:52=32+x2,
解得x=±4,
∴点P的坐标为(4,-7)(-4,-7).
故本题答案为:(4,-7)或(-4,-7).
点评:圆心在弦的垂直平分线上,本题根据勾股定理得到方程,就可以求出圆心的坐标.
分析:设点P的横坐标是x,过P作PE⊥MN,则点P在MN的垂直平分线上,点P的横坐标是-7,设点P的横坐标是x,在Rt△MPE中,根据勾股定理得:MP2=ME2+PE2,故可求得PE的长.
解答:
 解:点P在MN的垂直平分线上,点M(0,-4),N(0,-10),
解:点P在MN的垂直平分线上,点M(0,-4),N(0,-10),∴点P的纵坐标是-7,
设点P的横坐标是x,过P作PE⊥MN,
在△MPE中根据勾股定理得到MP2=ME2+PE2,
即:52=32+x2,
解得x=±4,
∴点P的坐标为(4,-7)(-4,-7).
故本题答案为:(4,-7)或(-4,-7).
点评:圆心在弦的垂直平分线上,本题根据勾股定理得到方程,就可以求出圆心的坐标.

练习册系列答案
相关题目
 如图,已知半径为1的⊙O1与x轴交于A,B两点,OM为⊙O1的切线,切点为M,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A,B两点.
如图,已知半径为1的⊙O1与x轴交于A,B两点,OM为⊙O1的切线,切点为M,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A,B两点.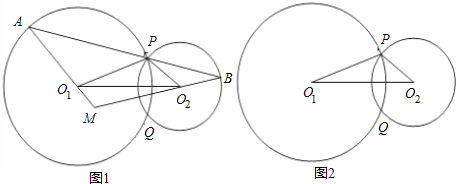
 如图,已知半径为1的⊙O1与x轴交于A,B两点,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A,B两点.
如图,已知半径为1的⊙O1与x轴交于A,B两点,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A,B两点. 单位的速度向下平移,设运动时间为t(t>0),求t为何值时,直线MN再一次与⊙O1相切?(本小题保留3位有效数字)
单位的速度向下平移,设运动时间为t(t>0),求t为何值时,直线MN再一次与⊙O1相切?(本小题保留3位有效数字)