题目内容
如图在△ABC中，∠B=40°，∠C=70°，AD⊥BC于D，AE平分∠BAC交BC于E，则∠DAE等于
- A.70°
- B.35°
- C.15°
- D.20°
C
分析：根据角平分线上的任意一点到角的两边距离相等计算．
解答：由已知可得，∠BAC=180°-40°-70°=70°，∠CAD=20°，
∴∠DAE=∠CAE-∠CAD=35°-20°=15°．
故选C．
点评：此题主要考查角平分线的性质三角形的内角和定理．
分析：根据角平分线上的任意一点到角的两边距离相等计算．
解答：由已知可得，∠BAC=180°-40°-70°=70°，∠CAD=20°，
∴∠DAE=∠CAE-∠CAD=35°-20°=15°．
故选C．
点评：此题主要考查角平分线的性质三角形的内角和定理．
练习册系列答案
相关题目
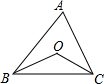如图在△ABC中，∠ABC=50°，∠ACB=75°，点O是内心，则∠BOC的度数为
如图在△ABC中，∠A=45°，tanB=3，BC=
已知，如图在△ABC中，AD是BC边上的高线，CE是AB边上的中线，DG平分∠CDE，DC=AE，
如图在△ABC中，AD垂直平分BC，AD=8，BC=10，E、F是AD上的两点，则图中阴影部分的面积是