题目内容
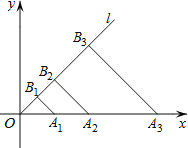
【题目】如图，在平面直角坐标系xOy中，点A1，A2，A3，…，An在x轴的正半轴上，且OA1=2，OA2=2OA1，OA3=2OA2，…，OAn=2OAn﹣1，点B1，B2，B3，…，Bn在第一象限的角平分线l上，且A1B1，A2B2，…，AnBn都与射线l垂直，则B1的坐标是 ，B3的坐标是 ，Bn的坐标是 ．
【答案】（1，1）；（4，4）；（
，）．
【解析】
试题分析：如图，由题意知，△OAnBn是等腰直角三角形，根据规律得出OA1=2，OA2=4，OA3=8，OA4=16，OA5=32，所以可得OAn=
，∴所以Bn的坐标为（
，）即（，），∴B1的坐标是（1，1），B3的坐标是（4，4），Bn的坐标是（，）．故答案为：（1，1）；（4，4）；（，）．
练习册系列答案
相关题目
