题目内容
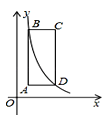
如图,矩形ABCD的边AB与y轴平行,顶点A的坐标为(1,2),点B和点D在反比例函数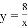 (x>0)的图象上,则矩形ABCD的面积为_________.
(x>0)的图象上,则矩形ABCD的面积为_________.
练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
题目内容
如图,矩形ABCD的边AB与y轴平行,顶点A的坐标为(1,2),点B和点D在反比例函数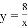 (x>0)的图象上,则矩形ABCD的面积为_________.
(x>0)的图象上,则矩形ABCD的面积为_________.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案