题目内容
先化简,再求值:(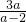 -
- )×
)×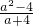 -2,其中a=
-2,其中a= -1.
-1.
解:(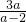 -
- )×
)×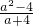 -2
-2
=[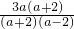 -
- ]×
]×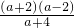 -2
-2
=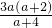 -
-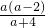 -2
-2
=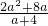 -2
-2
=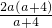 -2
-2
=2a-2,
当a= -1时,原式=2(
-1时,原式=2( -1)-2=2
-1)-2=2 -4.
-4.
分析:找出括号中两分母得最简公分母,通分后利用乘法分配律化简,约分后利用分式的减法法则:分母不变只把分子相减,然后分子提取2a,分解因式后再与分母约分,得出原式的最简结果,最后把a的值代入,化简即可得到原式的值.
点评:此题考查了分式的化简求值,分式的化简求值,加减法关键是通分,通分的关键是找出各分母的最简公分母,分式的乘除法关键是约分,约分的关键是找出公因式,若出现多项式,应将多项式分解因式后再约分,在化简过程中有时利用法则计算后,分子分母继续分解因式,还能约分,做题时要注意.同时注意化简求值题常常把原式化为最简,然后再代值.
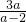 -
- )×
)×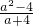 -2
-2=[
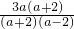 -
- ]×
]×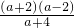 -2
-2=
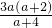 -
-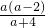 -2
-2=
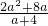 -2
-2=
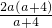 -2
-2=2a-2,
当a=
 -1时,原式=2(
-1时,原式=2( -1)-2=2
-1)-2=2 -4.
-4.分析:找出括号中两分母得最简公分母,通分后利用乘法分配律化简,约分后利用分式的减法法则:分母不变只把分子相减,然后分子提取2a,分解因式后再与分母约分,得出原式的最简结果,最后把a的值代入,化简即可得到原式的值.
点评:此题考查了分式的化简求值,分式的化简求值,加减法关键是通分,通分的关键是找出各分母的最简公分母,分式的乘除法关键是约分,约分的关键是找出公因式,若出现多项式,应将多项式分解因式后再约分,在化简过程中有时利用法则计算后,分子分母继续分解因式,还能约分,做题时要注意.同时注意化简求值题常常把原式化为最简,然后再代值.

练习册系列答案
相关题目