题目内容
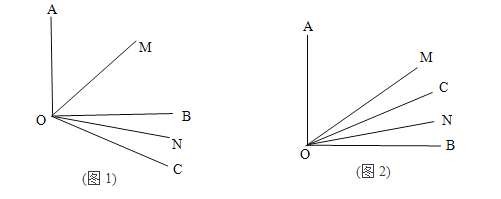
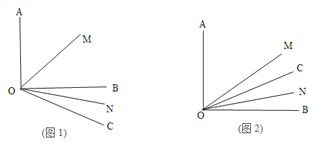
【题目】已知∠AOB=90°,![]() 是锐角,ON平分
是锐角,ON平分![]() ,OM平分∠AOB.
,OM平分∠AOB.
(1)如图1若![]() =30°,求
=30°,求![]() 的度数?
的度数?
(2)若射线OC绕着点O运动到∠AOB的内部(如图2),在(1)的条件下求![]() 的度数;
的度数;
(3)若∠AOB=![]() (90°≤
(90°≤![]() <180°),
<180°),![]() =
= ![]() (0°<
(0°<![]() <90°),请用含有
<90°),请用含有![]() 的式子直接表示上述两种情况
的式子直接表示上述两种情况![]() 的度数.
的度数.
【答案】(1)60°;(2)30°;(3)①∠MON=![]() (
(![]() +
+![]() ),;②∠MON=
),;②∠MON=![]() (
(![]() -
-![]() ).
).
【解析】试题分析:(1)由于∠AOB=90°,∠BOC=30°,OM平分∠AOB,ON平分∠BOC,所以可以求得∠MOB和∠NOB的度数,进而求得∠MON的度数;(2)类比(1)的方法求解即可;(3)结合(1)(2)题的计算方法求解即可.
试题解析:
(1)∵OM平分∠AOB,ON平分∠BOC,
∴∠BOM=![]() ∠AOB,∠BON=
∠AOB,∠BON=![]() ∠BOC.
∠BOC.
∵∠AOB=90°,∠BOC=30°,
∴∠BOM=![]() ×90°=45°,∠BON=
×90°=45°,∠BON=![]() ×30°=15°,
×30°=15°,
∴∠MON=∠BOM+∠BON=45°+15°=60°.
(2)由(1)可知:∠BOM=45°,∠BON=15°,
∴∠MON=∠BOM-∠BON=45°-15°=30°.
(3)①∠MON=![]() (
(![]() +
+![]() ),②∠MON=
),②∠MON=![]() (
(![]() -
-![]() ).
).
点睛:本题主要考查学生角平分线的定义及角的计算的理解和掌握,在解决角与角之间的关系时,要充分利用已知条件和图中的隐含条件.
【题型】解答题
【结束】
27
【题目】(1)已知线段AB=8cm,在线段AB上有一点C,且BC=4cm,M为线段AC的中点.
①求线段AM的长?
②若点C在线段AB的延长线上,AM的长度又是多少呢?
(2)如图,AD=![]() DB,E是BC的中点,BE=
DB,E是BC的中点,BE=![]() AC=2cm,求DE的长.
AC=2cm,求DE的长.
![]()
【答案】(1)①2㎝;②6㎝;(2)6㎝.
【解析】试题分析:(1)①根据题意画出图形,先求得线段AC的长,再根据线段中点的定义求得AM的长即可;②根据题意画出图形,先求得线段AC的长,再根据线段中点的定义求得AM的长即可;(2)根据已知条件求得AC的长,再由线段中点的定义求得BC的长,即可求得AB的长;再由线段和差倍分之间的关系求解即可.
试题解析:
(1)①∵AB=8cm,BC=4cm,
∴AC=AB-BC=8-4=4cm.
∵M是AC的中点,
∴AM=![]() AC=
AC=![]() ×4=2cm.
×4=2cm.
![]()
②∵AB=8cm,BC=4cm,
∴AC=AB+BC=8+4=12cm.
∵M是AC的中点,
∴AM=![]() AC=6cm.
AC=6cm.
![]()
(2)∵BE=![]() AC=2cm,∴AC=10cm.
AC=2cm,∴AC=10cm.
∵E是BC的中点,∴BC=2BE=4cm,∴AB=AC-BC=10-4=6cm.
∵AD=![]() BD,AD+BD=AB,∴
BD,AD+BD=AB,∴![]() BD+BD=AB=6cm,∴BD=4cm,∴DE=BD+BE=4+2=6cm.
BD+BD=AB=6cm,∴BD=4cm,∴DE=BD+BE=4+2=6cm.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案