题目内容
【题目】如图Rt△ABC中,∠ACB=90°,D为AB的中点,E在边AB上,AB=12,BC=6,当ED= ![]() CD,则CE= .
CD,则CE= . 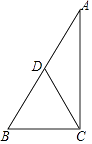
【答案】3 ![]() 或3
或3 ![]()
【解析】解:∵在Rt△ABC中,∠ACB=90°,D为AB的中点,AB=12,BC=6,
∴AD=BD=CD= ![]() AB=6,①如图1,E在AD上,
AB=6,①如图1,E在AD上,
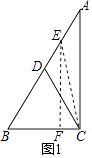
连结CE,过E点作EF⊥BC于F,
∵ED= ![]() CD,
CD,
∴DE=3,
∴BE=9,
∴BF= ![]() BE=4.5,
BE=4.5,
∴在Rt△BFE中,EF= ![]() =
= ![]() ,
,
∵CF=BC﹣BF=6﹣4.5=1.5,
∴在Rt△CFE中,CE= ![]() =3
=3 ![]() ;②如图2,E在BD上,
;②如图2,E在BD上,
连结CE,过E点作EF⊥BC于F,
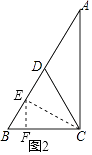
∵ED= ![]() CD,
CD,
∴DE=3,
∴BE=3,
∴BF= ![]() BE=1.5,
BE=1.5,
∴在Rt△BFE中,EF= ![]() =
= ![]() ,
,
∵CF=BC﹣BF=6﹣1.5=4.5,
∴在Rt△CFE中,CE= ![]() =3
=3 ![]() .
.
故CE=3 ![]() 或3
或3 ![]() .
.
所以答案是:3 ![]() 或3
或3 ![]() .
.
【考点精析】本题主要考查了直角三角形斜边上的中线和勾股定理的概念的相关知识点,需要掌握直角三角形斜边上的中线等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目