Question

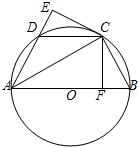29、已知：如图，AB是⊙O的直径，点C、D为圆上两点，且弧CB=弧CD，CF⊥AB于点F，CE⊥AD的延长线于点E．求证：DE=BF．

Answer 1

分析：由弧CB=弧CD，根据圆周角定理得到CB=CD，∠CAE=∠CAB，而CF⊥AB，CE⊥AD，根据角平分线定理得到CE=CF，于是有Rt△CED≌Rt△CFB，即可得到结论．

解答：证明：∵弧CB=弧CD，
∴CB=CD，∠CAE=∠CAB，
又∵CF⊥AB，CE⊥AD，
∴CE=CF，
∴Rt△CED≌Rt△CFB，
∴DE=BF．

点评：本题考查了在同圆或等圆中，如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等，则另外两组量也对应相等．也考查了圆周角定理、角平分线定理以及三角形全等的判定与性质．