题目内容
(14分)已知抛物线 经过A(3,0), B(4,1)两点,且与y轴交于点C.
经过A(3,0), B(4,1)两点,且与y轴交于点C.
(1)求抛物线 的函数关系式及点C的坐标;
的函数关系式及点C的坐标;
(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点P,使△PAB是以AB为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求点E的坐标.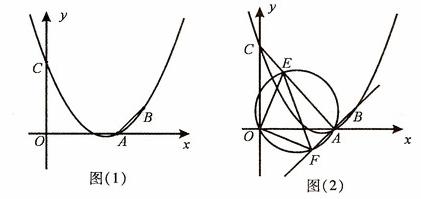
解:(1)(3分)将A(3,0),B(4,1)代人
得
∴
∴
∴C(0,3)
(2)(7分)假设存在,分两种情况,如图.
①连接AC,
∵OA="OC=3," ∴∠OAC=∠OCA=45O. ……1分
过B作BD⊥ 轴于D,则有BD=1,
轴于D,则有BD=1, ,
,
∴BD="AD," ∴∠DAB=∠DBA=45O.
∴∠BAC=180O-45O-45O=90O……………2分
∴△ABC是直角三角形. ∴C(0,3)符合条件.
∴P1(0,3)为所求.
②当∠ABP=90O时,过B作BP∥AC,BP交抛物线于点P.
∵A(3,0),C(0,3)
∴直线AC的函数关系式为
将直线AC向上平移2个单位与直线BP重合.
则直线BP的函数关系式为
由 ,得
,得
又B(4,1), ∴P2(-1,6).
综上所述,存在两点P1(0,3), P2(-1,6).
另解②当∠ABP=90O时, 过B作BP∥AC,BP交抛物线于点P.
∵A(3,0),C(0,3)
∴直线AC的函数关系式为
将直线AC向上平移2个单位与直线BP重合.
则直线BP的函数关系式为
∵点P在直线 上,又在
上,又在 上.
上.
∴设点P为
∴
解得
∴P1(-1,6), P2(4,1)(舍)
综上所述,存在两点P1(0,3), P2(-1,6).
(3)(4分) ∵∠OAE=∠OAF=45O,而∠OEF=∠OAF=45O,
∠OFE=∠OAE=45O,
∴∠OEF=∠OFE=45O,
∴OE="OF," ∠EOF=90O
∵点E在线段AC上,
∴设E
∴
=
∴
=
=
=
∴当 时,
时,  取最小值,
取最小值,
此时 ,
,
∴
解析

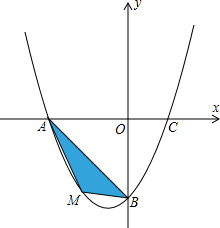 在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),
在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),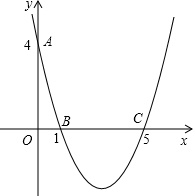 如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.
如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.