题目内容
（2011•锦州）有甲、乙两个不透明口袋，每个口袋里装有四个小球（小球除字母不同外，其余均相同），甲袋中的四个小球上分别写着字母“g”“o”“o”“d”，乙袋中的四个小球上分别写着字母“l”“u”“c”“k”，小红从每个口袋中各随机摸出一球．
（1）请用列表法（或画树状图）表示小红摸出的所有可能结果．
（2）求小红刚好摸到“o”和“k”的概率．
（1）请用列表法（或画树状图）表示小红摸出的所有可能结果．
（2）求小红刚好摸到“o”和“k”的概率．
分析：（1）列表求出所有的情况数即可解答．
（2）根据上题得到的情况数结合概率公式计算即可解答．
（2）根据上题得到的情况数结合概率公式计算即可解答．
解答：解：（1）列表如下：
由列表可知，共有16种可能的结果，并且每种结果出现的可能性相同．（7分）
（2）共有16种可能的结果，其中刚好能摸到“o”“k”的有2种．
P（摸到“o”“k”）=
=
．（10分）
| 乙 | ||||
| 甲 | l | u | c | k |
| g | （g，l） | （g，u） | （g，c） | （g，k） |
| o | （o，l） | （o，u） | （o，c） | （o，k） |
| o | （o，l） | （o，u） | （o，c） | （o，k） |
| d | （d，l） | （d，u） | （d，c） | （d，k） |
（2）共有16种可能的结果，其中刚好能摸到“o”“k”的有2种．
P（摸到“o”“k”）=
| 2 |
| 16 |
| 1 |
| 8 |
点评：考查用列树状图的方法解决概率问题；得到所有的情况数是解决本题的关键；用到的知识点为：概率等于所求情况数与总情况数之比．
练习册系列答案
名校课堂系列答案
相关题目
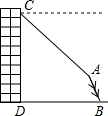（2011•锦州）如图，小明站在窗口向外望去，发现楼下有一棵倾斜的大树，在窗口C处测得大树顶部A的俯角为45°，若已知∠ABD=60°，CD=20m，BD=16m，请你帮小明计算一下，如果大树倒在地面上，其顶端A与楼底端D的距离是多少米？（结果保留整数，参考数据：
出结论；若不成立，请说明理由．
梯形？若存在，求出此刻的t值；若不存在，请说明理由．