题目内容

如右图，正方形ABCD内接于半径为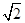的⊙O，E为DC的中点，连接BE，则点O到BE的距离等于_________．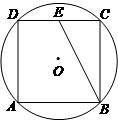

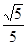
解析试题分析：根据内接正方形的性质可求得正方形的边长，再根据勾股定理结合E为DC的中点即可求得BE的长，作OQ⊥EB于点Q，连接OE，则可证得△OQE∽△ECB，根据相似三角形的性质即可求得结果.
由题意得正方形ABCD的边长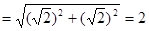
∵E为DC的中点
∴
∴
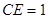
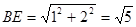
作OQ⊥EB于点Q，连接OE，
则△OQE∽△ECB
∴
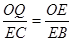
即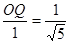
解得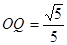
则点O到BE的距离等于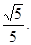
考点：正方形的性质，勾股定理，相似三角形的判定和性质
点评：解答本题的关键是熟练掌握相似三角形的对应边成比例，注意对应字母在对应位置上.

练习册系列答案
相关题目
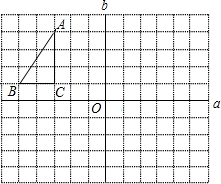
精英家教网如右图，每个小正方形的边长都是1，△ABC的三个顶点都在格点处，则△ABC的面积是（　　）
A、4B、5C、7D、8
在如右图所示的方格图中，我们称每个小正方形的顶点为“格点”（小正方形的边长设为1个长度单位），以格点为顶点的三角形叫做“格点三角形”．根据图形，解决下面的问题：
（1）把格点△ABC向右平移6个长度单位，得△A′B′C′，请画出该三角形；
（2）以a、b交点O为对称中心，画出△A′B′C′关于点O的中心对称图形△A″B″C″；
（3）如果以直线a、b为坐标轴建立平面直角坐标系后，点A的坐标为（-3，4）精英家教网，请写出△A″B″C″各顶点的坐标，并求出△A″B″C″的周长（结果用根号表示）．

（6分）如右图，方格纸中小正方形的边长为1，△ABC的三个顶点都在小正方形的格点上，求

（1）△ABC的面积；

（2）△ABC的周长；

（3）点C到AB边的距离．

 

（6分）如右图，方格纸中小正方形的边长为1，△ABC的三个顶点都在小正方形的格点上，求

（1）△ABC的面积；

（2）△ABC的周长；

（3）点C到AB边的距离．

 

在方格纸(每个小方格都是边长为单位长度的正方形)中，我们称每个小正方形的顶点为格点，以格点为顶点的图形叫格点图形．如右图中的△ABC叫格点△ABC．

(1)如果A、D两点的坐标分别为(1，1)和(0，一1)，请你在方格纸中建立平面直角坐标系，并直接写出B、C点的坐标：

(2)请根据你学过的平移、旋转或对称等知识，说明图中的“格点四边形”图案是怎样通过“格点△ABC”变换得到的?

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网