题目内容
 如图四边形ABCD内接于圆,CB=CD.两个动点E﹑F各在AC﹑AD上,且满足EF∥BD,设BE交CF于点P,则点P的几何位置是
如图四边形ABCD内接于圆,CB=CD.两个动点E﹑F各在AC﹑AD上,且满足EF∥BD,设BE交CF于点P,则点P的几何位置是
- A.在圆外
- B.在圆内
- C.在圆上
- D.不能确定
C
分析:根据同圆中相等的弦所对的弧相等以及同弧和等弧所对的圆周角相等,可以得到△ABC∽△AKD,得到对应线段成比例,根据EF∥BD,把对应的线段转化,得到△ABE∽△ACF,两相似三角形对应角相等,得到∠BPC是圆的一个圆周角,判断点P在圆上.
解答:由CB=CD得∠BAC=∠CAD,从而△ABC∽△AKD,故
∴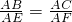
于是△ABE∽△ACF
∴∠ACP=∠ABE
∴∠BAC=∠CPB
∴P在圆上
点评:本题考查的是点与圆的位置关系,根据题意判断三角形相似,然后由三角形相似对应角相等,以及圆周角的概念判断点P的位置.
分析:根据同圆中相等的弦所对的弧相等以及同弧和等弧所对的圆周角相等,可以得到△ABC∽△AKD,得到对应线段成比例,根据EF∥BD,把对应的线段转化,得到△ABE∽△ACF,两相似三角形对应角相等,得到∠BPC是圆的一个圆周角,判断点P在圆上.
解答:由CB=CD得∠BAC=∠CAD,从而△ABC∽△AKD,故

∴
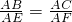
于是△ABE∽△ACF
∴∠ACP=∠ABE
∴∠BAC=∠CPB
∴P在圆上
点评:本题考查的是点与圆的位置关系,根据题意判断三角形相似,然后由三角形相似对应角相等,以及圆周角的概念判断点P的位置.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 17、如图四边形ABCD内接于⊙O,AB为直径,PD切⊙O于D,与BA延长线交于P点,已知∠BCD=130°,则∠ADP=
17、如图四边形ABCD内接于⊙O,AB为直径,PD切⊙O于D,与BA延长线交于P点,已知∠BCD=130°,则∠ADP=


