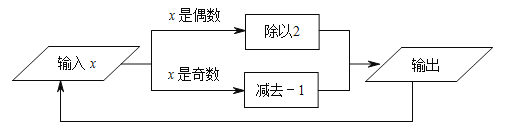
题目内容
【题目】如图，在矩形ABCD中，AB=4，BC=3，点O为对角线BD的中点，点P从点A出发，沿折线AD﹣DO﹣OC以每秒1个单位长度的速度向终点C运动，当点P与点A不重合时，过点P作PQ⊥AB于点Q，以PQ为边向右作正方形PQMN，设正方形PQMN与△ABD重叠部分图形的面积为S（平方单位），点P运动的时间为t（秒）．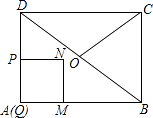 
（1）求点N落在BD上时t的值；
（2）直接写出点O在正方形PQMN内部时t的取值范围；
（3）当点P在折线AD﹣DO上运动时，求S与t之间的函数关系式；
（4）直接写出直线DN平分△BCD面积时t的值．
【答案】
（1）解：当点N落在BD上时，如图1．
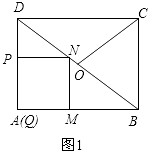
∵四边形PQMN是正方形，
∴PN∥QM，PN=PQ=t．
∴△DPN∽△DQB．
∴ 
．
∵PN=PQ=PA=t，DP=3﹣t，QB=AB=4，
∴ 
．
∴t= 
．
∴当t= 时，点N落在BD上
（2）解：①如图2，
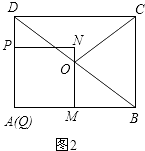
则有QM=QP=t，MB=4﹣t．
∵四边形PQMN是正方形，
∴MN∥DQ．
∵点O是DB的中点，
∴QM=BM．
∴t=4﹣t．
∴t=2．
②如图3，
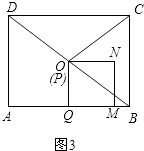
∵四边形ABCD是矩形，
∴∠A=90°．
∵AB=4，AD=3，
∴DB=5．
∵点O是DB的中点，
∴DO= 
．
∴1×t=AD+DO=3+ ．
∴t= 
．
∴当点O在正方形PQMN内部时，t的范围是2＜t＜
（3）解：①当0＜t≤ 时，如图4．
S=S正方形PQMN=PQ2=PA2=t2．
②当 ＜t≤3时，如图5，
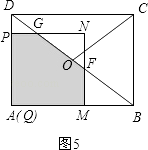
∵tan∠ADB= 
= 
，
∴ 
= 
．
∴PG=4﹣ t．
∴GN=PN﹣PG=t﹣（4﹣ t）= 
﹣4．
∵tan∠NFG=tan∠ADB= ，
∴ 
．
∴NF= 
GN= （ ﹣4）= 
t﹣3．
∴S=S正方形PQMN﹣S△GNF
=t2﹣ 
×（ ﹣4）×（ t﹣3）
=﹣ 
t2+7t﹣6．
③当3＜t≤ 时，如图6，
∵四边形PQMN是正方形，四边形ABCD是矩形．
∴∠PQM=∠DAB=90°．
∴PQ∥AD．
∴△BQP∽△BAD．
∴ 
．
∵BP=8﹣t，BD=5，BA=4，AD=3，
∴ 
．
∴BQ= 
，PQ= 
．
∴QM=PQ= ．
∴BM=BQ﹣QM= 
．
∵tan∠ABD= 
，
∴FM= BM= 
．
∴S=S梯形PQMF= （PQ+FM）QM
= [ + ]
= 
（8﹣t）2
= 
t2﹣ 
t+ 
．
综上所述：当0＜t≤ 时，S=t2．
当 ＜t≤3时，S=﹣ t2+7t﹣6．
当3＜t≤ 时，S= t2﹣ t+
（4）解：设直线DN与BC交于点E，
∵直线DN平分△BCD面积，
∴BE=CE= 
．
①点P在AD上，过点E作EH∥PN交AD于点H，如图7，
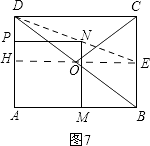
则有△DPN∽△DHE．
∴ 
．
∵PN=PA=t，DP=3﹣t，DH=CE= ，EH=AB=4，
∴ 
．
解得；t= 
．
②点P在DO上，连接OE，如图8，
则有OE=2，OE∥DC∥AB∥PN．
∴△DPN∽△DOE．
∴ 
．
∵DP=t﹣3，DO= ，OE=2，
∴PN= 
（t﹣3）．
∵PQ= 
（8﹣t），PN=PQ，
∴ （t﹣3）= （8﹣t）．
解得：t= 
．
③点P在OC上，设DE与OC交于点S，连接OE，交PQ于点R，如图9，
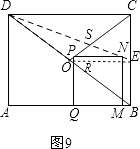
则有OE=2，OE∥DC．
∴△DSC∽△ESO．
∴ 
．
∴SC=2SO．
∵OC= ，
∴SO= 
= 
．
∵PN∥AB∥DC∥OE，
∴△SPN∽△SOE．
∴ 
．
∵SP=3+ + ﹣t= 
，SO= ，OE=2，
∴PN= 
．
∵PR∥MN∥BC，
∴△ORP∽△OEC．
∴ 
．
∵OP=t﹣ ，OC= ，EC= ，
∴PR= 
．
∵QR=BE= ，
∴PQ=PR+QR= 
．
∵PN=PQ，
∴ = ．
解得：t= 
．
综上所述：当直线DN平分△BCD面积时，t的值为 、 、 ．
【解析】（1）可证△DPN∽△DQB，从而有 ，即可求出t的值．（2）只需考虑两个临界位置（①MN经过点O，②点P与点O重合）下t的值，就可得到点O在正方形PQMN内部时t的取值范围．（3）根据正方形PQMN与△ABD重叠部分图形形状不同分成三类，如图4、图5、图6，然后运用三角形相似、锐角三角函数等知识就可求出S与t之间的函数关系式．（4）由于点P在折线AD﹣DO﹣OC运动，可分点P在AD上，点P在DO上，点P在OC上三种情况进行讨论，然后运用三角形相似等知识就可求出直线DN平分△BCD面积时t的值．
