Question

【题目】如图，Rt△ABC中，∠B＝90°，∠ACB＝30°，BC＝，点D在边BC上，连接AD，在AD上方作等边三角形ADE，连接EC．

(1)求证：DE＝CE；

(2)若点D在BC延长线上，其他条件不变，直接写出DE，CE之间的数量关系(不必证明)；

(3)当点D从点B出发沿着线段BC运动到点C时，求点E的运动路径长．

Answer 1

【答案】（1）证明见解析；（2）DE，CE之间的数量关系为：；（3）点E的运动路径长为.

【解析】

（1）如图（见解析），取AC的中点F，连接BF、EF，利用直角三角形和等边三角形的性质推出，再由全等三角形的性质得，根据等腰三角形三线合一的性质得是等腰三角形，则有，又因，即可得证；

（2）如图（见解析），取AC的中点G，连接BG、EG，利用直角三角形和等边三角形的性质推出，再由全等三角形的性质得，根据等腰三角形三线合一的性质得是等腰三角形，则有，又因，从而可得；

（3）先确定点E的运动路径，再利用直角三角形的性质和等边三角形的性质即可求得.

（1）如图，取AC的中点F，连接BF、EF

中，

是等边三角形

又是等边三角形

在和中，

是等腰三角形，且

，即；

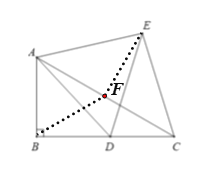
（2）DE，CE之间的数量关系为：，证明如下（注：考试时不要求）：

如图，取AC的中点G，连接BG、EG

中，

是等边三角形

又是等边三角形

在和中，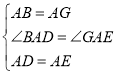

是等腰三角形，且

，即；

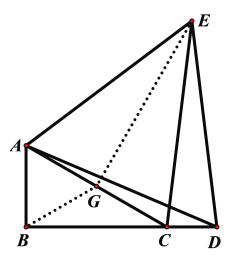
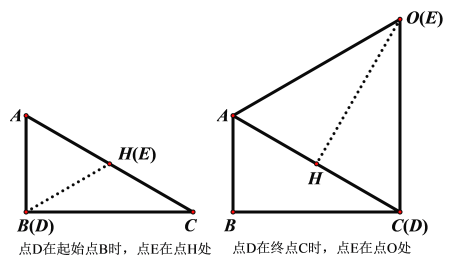
（3）如图，取AC的中点H，连接OH

由题（1）可知，当点D沿着线段BC运动时，一定是等腰三角形

即点E一定在AC的垂直平分线上

因此，当点D从点B出发沿着线段BC运动到点C时，点E是从点H出发沿着HO运动到点O，如图，HO即为所求

中，

由题意得，是等边三角形

由勾股定理得：

故所求的点E的运动路径长为.